안녕하세요. 오늘은 Heap에 대해 알아보려 합니다.
그 전에 지난 번에 아래와 같은 Tree를 그렸는데
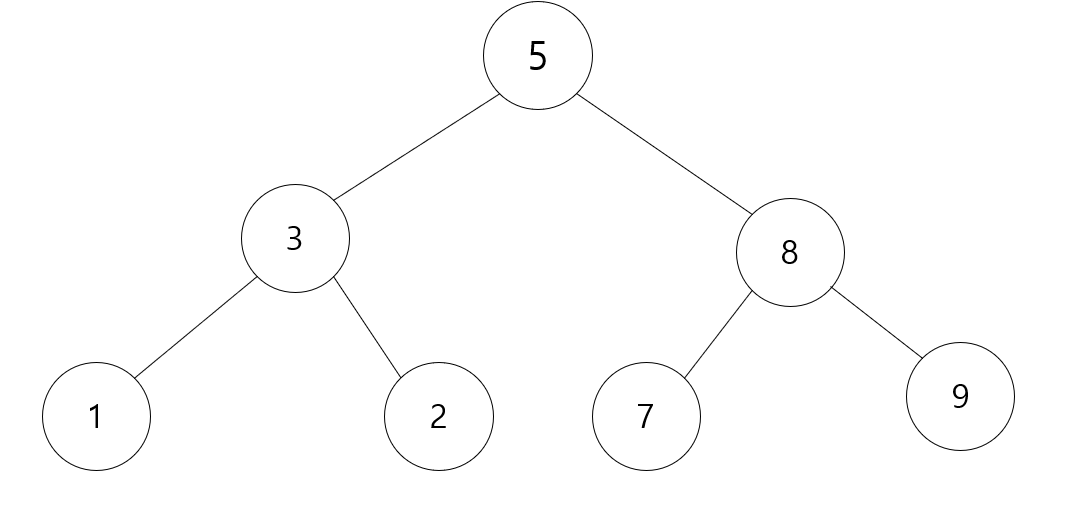
맨위의 root 값이 왜 5인지 궁금해 할 것입니다. 왜 가운데 값이 root에 들어갈까요?
생각해보면 1~10까지를 갖는 Tree가 있는데 아래와 같은 형태로 그려진다 했을 때
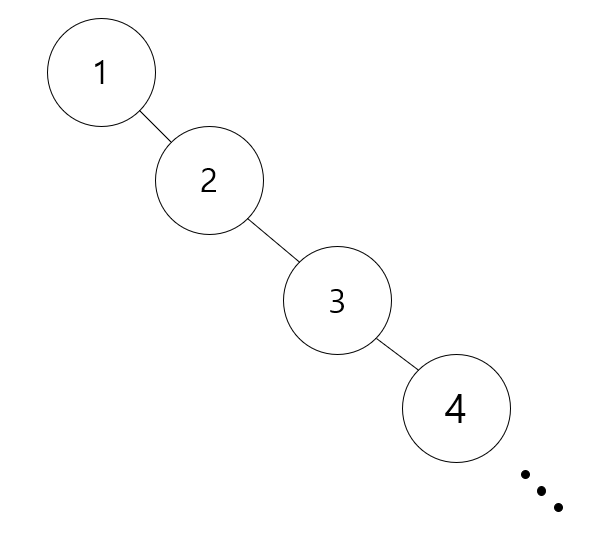
위와 같이 오른쪽으로만 이어진 Tree도 BST가 맞다. 자기 값보다 큰 값이 오른쪽이 들어가 있기 때문입니다.
그래서 1 ~ 10까지 Node를 집어 넣을 때 순서대로 집어 넣는다 할 때 위와 같이 한 줄로 나오게 됩니다.
반대로 10 ~ 1까지 거꾸로 집어넣으면 왼쪽으로만 값이 들어가질 것입니다.
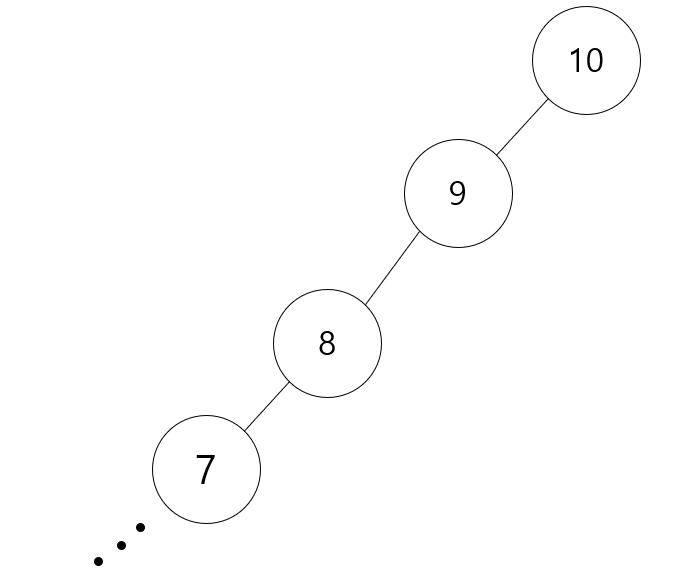
당연히 위의 형태도 BST가 맞습니다. 하지만 BST의 장점이 어떤 값을 찾을 때 반절을 버리고 찾는다는 것에 있는데
위의 형태에서 6을 찾는다 하면 버릴 Node들이 없어서 모든 Node들을 탐색하기 때문에 BST로서 갖는 이득이 없게 됩니다.
위의 형태로 찾을 때 O(N)의 속도를 갖게 됩니다. 그러므로 위와 같은 형태의 Tree도 BST이지만 잘못된, 비효율적인 BST가 됩니다.
이거를 효율적인 Tree로 바꾸려면 아래와 같이 가운데 값이 위에 올라가는 형태로 가야 합니다.

아까 비효율적인 Tree와 차이가 있다면 높이가 있다는 점입니다. BST에서는 높이(Depth)가 가장 적은 높이로 형성 되는 Tree가 가장 이상적인 Tree입니다.
그래서 이것을 최소 신장 트리 라고 합니다. 말 그대로 가장 작은 키(Depth)를 갖는 Tree라는 걸 의미하며 가장 효율적인 Tree라고 볼 수 있습니다.
그렇다면 이 최소 신장 트리는 어떻게 만들 수 있을까요?
여러 가지 방법이 있는데 그 중에서 AVL 트리 라고 있는데 Tree를 회전 시킨다고 생각하면 됩니다.

위와 같은 Tree가 있을 때 화살표 방향으로 회전 하게 되면 2가 올라가고 3이 내려가게 되어 아래와 같이 바뀌는데
최소 신장 트리의 형태로 바뀌게 됩니다. 위와 같이 AVL 트리 알고리즘을 사용하면 최소 신장 트리를 만들 수 있습니다.
그 외에도 Black Red 트리도 있습니다.
이제 다시 돌아와서 오늘 알아볼 부분은 Heap입니다. Heap에는 크게 최대Heap과 최소Heap이 있습니다.
차이라면 최대를 따지냐, 최소를 따지냐는 차이만 있을 뿐, 크게 차이는 없습니다.
최대Heap은 부모Node는 자식Node보다 항상 크거나 같아야 한다는 것이고, 최소Heap은 자식Node는 부모Node보다 항상 작거나 같아야 한다는 것을 의미 합니다.
같은 층에 있는 Node끼리는 대소관계는 없지만 부모, 자식간에는 크고 작음이 있어야 합니다.
Heap을 사용하면 최대 값과 최소 값을 찾기 좋습니다.
부모Node가 자식Node보다 크거나 같아야 하기 때문에 맨위에 있는 Node가 가장 큰 값이 되고, 자식Node는 부모Node보다 작거나 같아야 하기 때문에 가장 아래에 있는 Node가 최소값이 됩니다.
두번째로는 Priority Queue라고 해서 우선순위 큐 라고 하는데 이것을 Heap으로 만들 수 있습니다.
우선순위 큐는 우선순위대로 먼저 나온다는 것을 의미합니다. 큐는 들어간 순서대로 나오는 것을 의미하는데 우선순위가 높은 것이 먼저 나오게 됩니다.
예를 들어 응급실이 있고, 응급실의 대기열을 만든다고 가정할 때 응급실의 응급의 정도가 있을 것입니다.
어떤 사람은 빨리 치료해야하는 사람이 있을 수 있고, 어떤 사람은 기다려도 상관없는 사람이 있을 수 있을 것입니다.
그렇게 될 때 응급함의 값이 있을 때 그 값이 높은 것 부터 나오게 하고 싶을 때 쓰는게 Priority Queue입니다.
예를 들어 아래와 같은 Tree가 있을 때
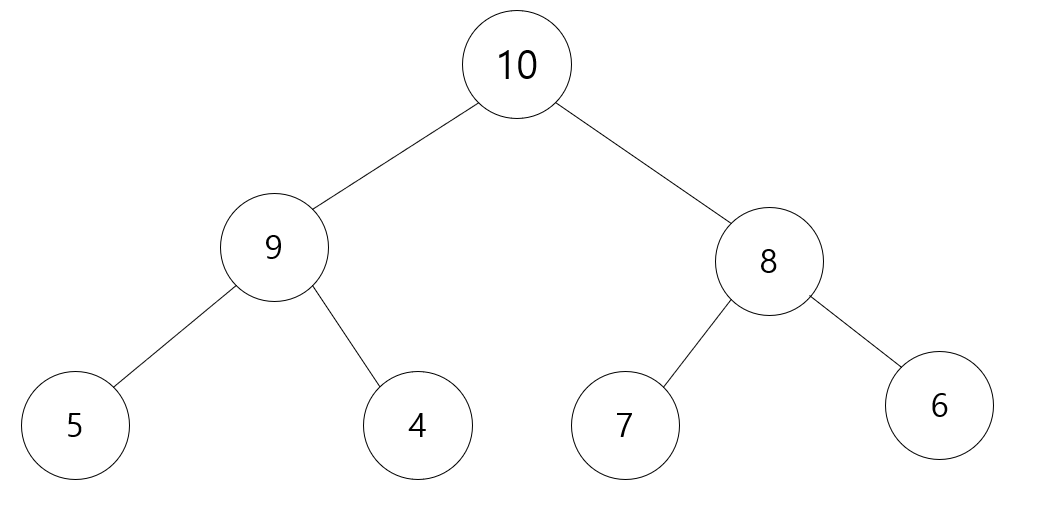
맨 위에 있는 값이 가장 급한 값이 된다. Heap은 그렇게 유지 되도록 만든 Tree입니다.
그래서 항상 맨위가 가장 크고, 맨 아래가 가장 작습니다.
그렇다면 이 Heap을 어떻게 만드는지 살펴보죠!
규칙은 위에 말했듯이 부모Node가 자식Node보다 크거나 같고, 자식Node는 부모Node보다 작거나 같습니다.
먼저 Heap Tree에 element추가(Push) 할 때 어떻게 하는지 알아보죠.
아래와 같이 Heap이 아래와 같이 구성되어 있을 때

여기서 새로 들어온 값이 생기면 맨 아래에 넣고, 새로 들어온 값이 부모Node보다 큰지 값을 비교를 합니다.
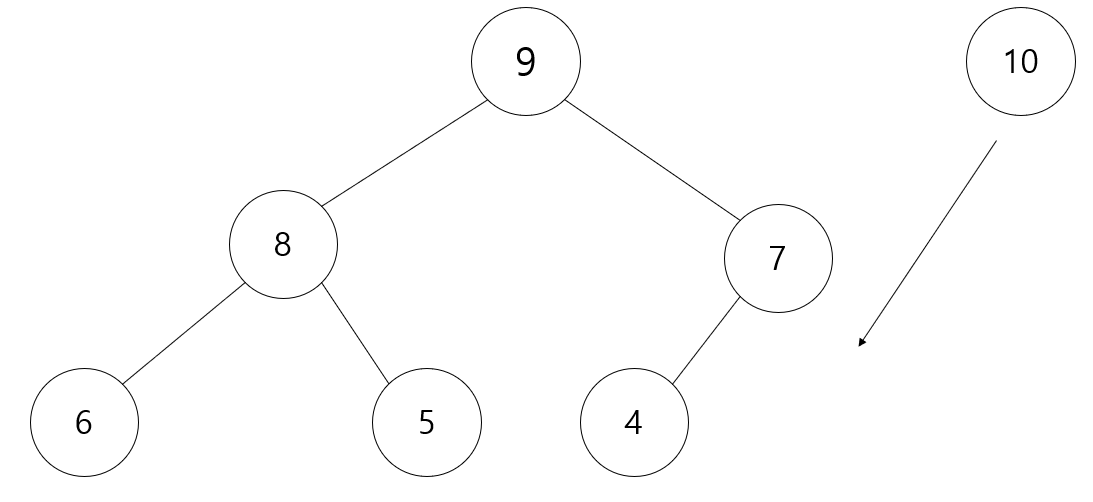

크다면 서로 위치를 바꾸어(Swap)줍니다.

그리고 또 다시 부모Node와 값을 비교해서 값이 크다면 위치를 바꾸어 줍니다.
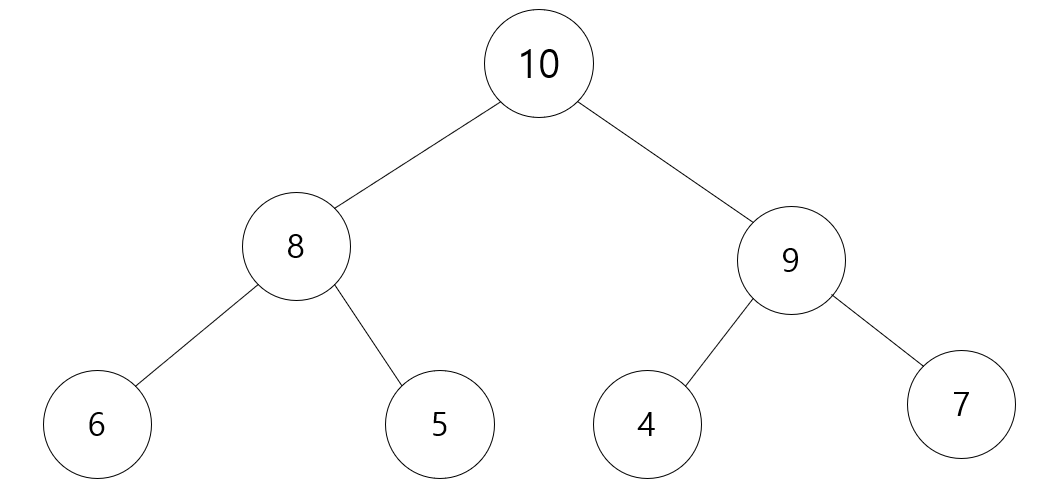
그래서 이것을 더 이상 못바꾸거나, 바꿀 부모Node가 없을 때 까지 반복 합니다.
그렇다면 항목 삭제는 어떻게 할까요? 항목 삭제는 Pop 이라고 하는데 맨 위부터 빠집니다.
최대 Heap은 가장 큰 값을 찾고, 최소Heap은 가장 작은 값을 찾기 때문에 큰 값부터 나오게 되는 것입니다.
아래와 같은 Tree가 있다고 가정하면

먼저 10이 빠져 나오게 됩니다.
그렇게 되면 빈자리가 생기고, 빈자리를 채워야 하는데 맨 끝에 있는 값을 맨 위로 올려줍니다.
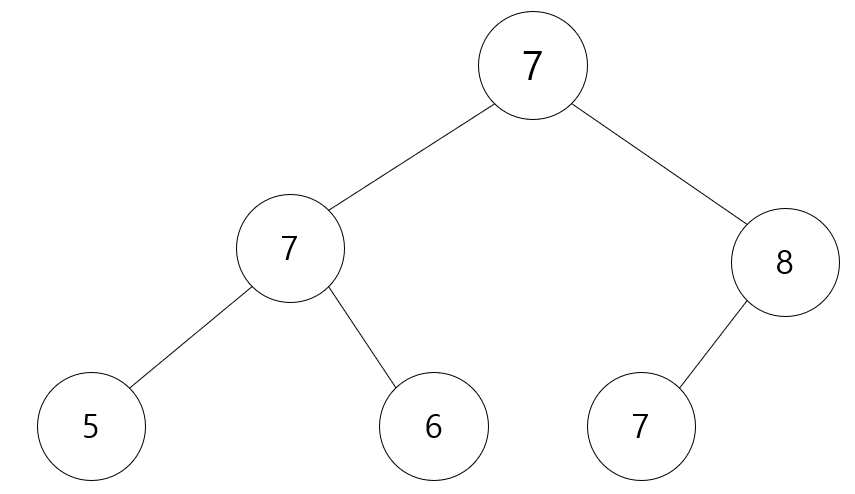
그 다음 맨 끝 부분이 없어지게 되고, 맨 위에 있는 값 기준으로 자기보다 큰 값이 존재하면 위치를 바꿉니다.
그래서 오른쪽에 있는 7과 8을 바꿉니다.
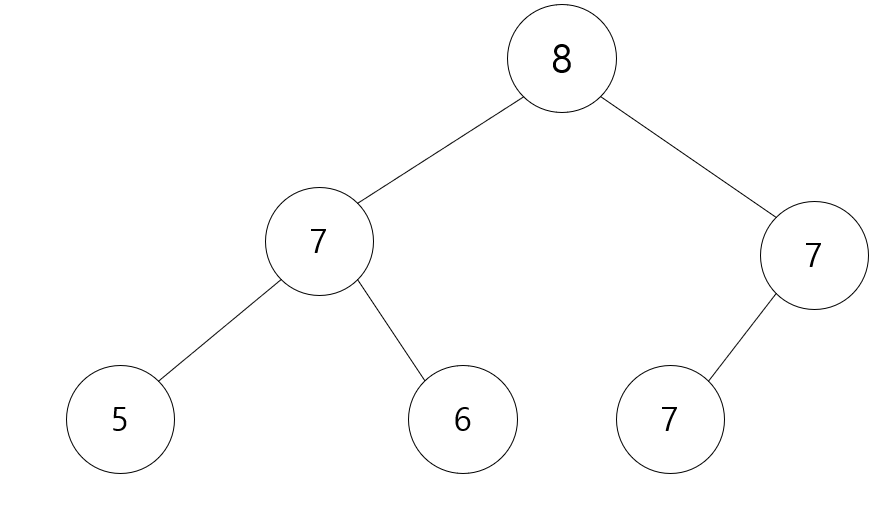
그 후 또 비교를 하여 자식Node 중에 자기보다 큰 값이 있는지 비교합니다.

맨 위에 값과 비교할 값이 없으면 빠진 쪽이 오른쪽이므로 오른쪽 부모(root)Node와 자식Node를 비교하여 큰 값이 있는지 비교해줍니다. 있으면 Swap을 해주고, 없으면 끝이 납니다.
이런식으로 계속 Pop을 진행하여 수를 빼내오면 큰 값부터 작은 값 순서대로 Sorting이 되게 됩니다.
그래서 Heap을 이용하면 정렬을 만들 수 있습니다.
그 다음 Heap의 속도를 알아보죠.
Heap의 속도를 볼 때 Push하는 게 있고, POP하는 게 있는데 Push부터 알아보자면
Push할 때는 맨 아래로 집어 넣고, 부모와 비교하여 Swap하는데 새로 들어온 값이 Swap해야 되는 반복횟수는 그 값의 층수에 비례됩니다.
예를 들어 아래와 같은 Tree가 있다고 가정하고 9가 새로 들어온 값일 때

9는 2번만 Swap하면 됩니다. 그러니까 층수 - 1번 반복이 되는 것이죠.
Heap을 이용하면 자동으로 최소신장트리가 만들어지는데 위의 Tree가 최소신장트리라고 했을 때 층수 - 1번의 층수는 전체 항목에서 2로 나눈 값입니다.
그러니까 지금 총 Node의 개수가 7개이고 2로 나누면 3, 3을 2로 나누면 1이니까 반절씩 없어진다고 볼 수 있는데 이 때 속도는 log2^N이 됩니다.
그래서 Heap에서의 Push의 속도는 O(log2^N)이 되고, POP을 보게 되면 맨위에 있는 걸 빼고 맨 아래 있는 것이 올라가면서 그 값이 내려가면서 비교하며 가기 때문에 위와 같이 층수 만큼 반복하기 때문에 O(log2^N)이 됩니다.
이제 Heap정렬의 속도를 보자. 10개의 항목이 무작위로 있다고 가정할 때
| 10 | 20 | 2 | 8 | 0 | 7 |
위의 값들을 Heap을 이용해 정렬한다 할 때 이 값들을 전부 Heap에 넣어야 하는데 각각 넣을 때마다 log2^N씩 들게
되어 Push할 때 10 * log2^10이 되고, Pop을 해야하기 때문에 마찬가지로 10 * log2^10이 들게 됩니다.
그래서 Push와 Pop을 하게 되면 2 * 10 * log2^10만큼 들게 되는데 여기서 10은 N이 되므로 다시 쓰게 되면
2 * N * log2^N이 됩니다. 그렇기 때문에 Heap 정렬은 O(2Nlog2^N)이 됩니다.
비고법에서 N이 엄청 크다고 가정할 때 (몇 억번 이라고 가정해보자) 그럴 때 N옆에 있는 2는 2* 를 의미 하는데 이것은 뒤의 N이 엄청 크게 되면 사실상 의미없는 수가 되어 버립니다.
그렇기 때문에 비고법에서 상수는 없애버리기 때문에 O(Nlog2^N)으로 말을 하기 때문에 Heap정렬에서의 속도는 O(Nlog2^N)가 됩니다.
여기까지가 Heap의 이론적인 부분이 끝이 났습니다.
'프로그래밍(Basic) > Golang' 카테고리의 다른 글
| [바미] Go - Heap 을 이용하여 문제를 풀어보자! (0) | 2021.02.09 |
|---|---|
| [바미] Go - Heap에 대해 알아보자2! (0) | 2021.02.01 |
| [바미] Go - BTS가 아닌 BST에 대해 알아보자! (0) | 2021.01.28 |
| [바미] Go - Tree BFS 와 Dijkstra에 대해 알아보자! (0) | 2021.01.26 |
| [바미] Go - Tree에 대해 알아보자! (0) | 2021.01.18 |