안녕하세요. 오늘은 이진트리에 대해 알아보고자 합니다.

위의 그림 같이 자식이 두 개 밖에 없는 것을 이진트리라고 합니다.
기존의 트리는
Type TreeNode struct {
childs []*TreeNode
}형태로 슬라이스 형태로 가졌는데 이진트리는 자식이 두 개 밖에 없기 때문에 슬라이스 형태로 가질 필요가 없습니다.
Type TreeNode Struct {
left *TreeNode
right *TreeNode
}이 부분을 코딩해보죠.
package dataStruct
type BinaryTreeNode struct {
Val int
left *BinaryTreeNode
right *BinaryTreeNode
}이 부분을 먼저 짚고 가는 이유는 다음에 설명할 BST(Binary Search Tree) 때문입니다.
BST는 이진 검색 트리가 Binary Tree로 되어 있기 때문입니다.
1~10까지 숫자가 있고, 5가 root라 가정할 때
left쪽은 root보다 작은 수, right쪽은 root보다 큰 수가 정렬 되어 있다. 이 규칙은 root에만 적용 되는게 아니라
모든 Node에 적용된다. 보면 2를 보면 2의 왼쪽값은 2보다 작은 수, 오른쪽은 2보다 큰 수가 있으며 8 또한 마찬가지 입니다.
left <= Parent <= right이런 규칙을 띄는 것을 알 수 있습니다.
이런 것을 이진 검색 트리 라고 할 수 있습니다.
이게 중요한 이유는 어떤 트리에서 어떤 값을 찾는다고 가정 했을 때

가령 위의 트리로 6이라는 값이 존재하는지 알아 볼 때 모든 트리를 다 검색하는 DFS나 BFS방법을 사용한 순회를 해야 합니다.
근데 BTS를 만들었다 가정했을 때
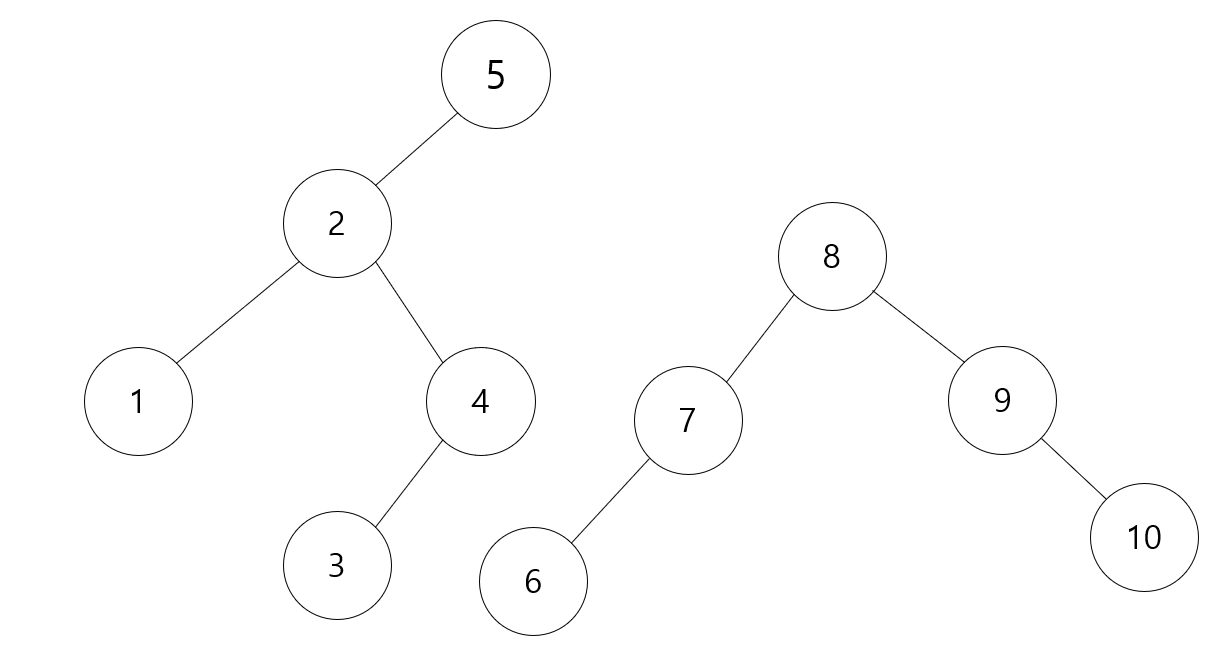
위 트리 안에 6이 있는지 찾으려 한다면 모든 노드를 다 가볼 필요가 없습니다.
먼저 현재 노드인 5와 비교를 먼저 합니다. 6은 root 노드인 5보다 크므로 6이라는 값이 있다면 오른쪽에 있을 것이며 왼쪽에 있는 트리는 볼 필요가 없습니다.
그 다음이 8인데 8은 6보다 작으므로 만약에 6이 존재한다면 왼쪽에 있을 것이므로 오른쪽 부분은 검사 대상에 제외 됩니다.
그 후 7이 나오는데 7은 6보다 작으므로 또 왼쪽으로 가게 되어 6을 찾게 됩니다.
그래서 이진검색트리는 어떤 값을 찾을 때 반절씩 버리며 가기 때문에 훨씬 빠르게 탐색 할 수 있습니다.
이제 속도를 살펴보죠.
일반적인 트리를 보았을 때 어떤 값이 있는지 찾으려면 모든 노드를 돌아보아야 한다고 했는데

여기서 6을 찾으려면 모든걸 다 거쳐 가봐야 합니다. 물론 운이 좋게 중간에 발견할 수 도 있겠지만 최악의 경우로 6이 아래와 같이 트리 안에 없다고 가정해보죠.
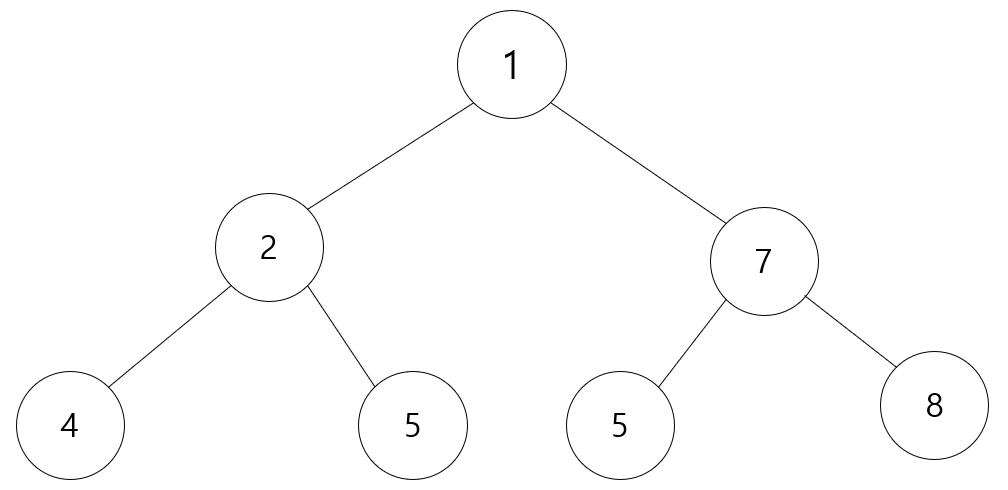
이 트리 안에 없다 쳐도 없는지 확인하려면 모든 노드들을 다 거쳐서 진짜 없는지 확인해야 합니다.
그렇다 했을 때 노드의 개수가 7개 이므로 반복문을 7번 돌아야 합니다.
항목의 개수만큼 반복문이 돌아야 하기 때문에 이 때는 O(N)의 속도를 갖게 됩니다.
그런데 이진 검색 트리를 살펴보자.

위의 트리에서 6을 찾는다 했을 때 3번 만에 6을 찾을 수 있습니다.
위의 노드의 개수가 7개인데 3번만에 찾았기 때문에 O(N)은 아닙니다.
그러면 6이 없을 때는 어떨까요?

5보다 크므로 오른쪽에 가고, 8보다 작으므로 왼쪽으로 가고, 7보다 작으므로 다음 노드로 갈 때 다음 노드가 없으므로 6이 없는 것을 알 수 있습니다. 이 때도 마찬가지로 3번에 알아냅니다.
그래서 이 때는 O(log2^N)이 됩니다.
아래의 화면은 그래프를 그리는 사이트에서 O(N)의 속도와 O(log2^N)의 속도를 측정해보기 위해 그린 그래프인데

첫번째 그래프(빨간색)은 y(갯수)가 늘어나면 x(시간)도 늘어나는 O(N)의 형태의 그래프이고, 두번째 그래프(파란색)은 O(log2^N)형태의 그래프인데 이를 통해 O(log2^N)은 O(N)에 비해 훨씬 빠르다는 것을 알 수 있습니다.
이제 이 부분을 코딩해보죠! binaryTree.go
package dataStruct
import "fmt"
type BinaryTreeNode struct {
Val int
left *BinaryTreeNode
right *BinaryTreeNode
}
type BinaryTree struct { // 1
Root *BinaryTreeNode
}
func NewBinaryTree(v int) *BinaryTree { // 3
tree := &BinaryTree{}
tree.Root = &BinaryTreeNode{Val: v}
return tree
}
func (n *BinaryTreeNode) AddNode(v int) *BinaryTreeNode { // 2
if n.Val < v { // 1
if n.left == nil { // 2
n.left = &BinaryTreeNode{Val: v}
return n.left
} else {
return n.left.AddNode(v) // 3
}
} else {
if n.right == nil { // 4
n.right = &BinaryTreeNode{Val: v} // 5
return n.right
} else { // 6
return n.right.AddNode(v)
}
}
}
1 : tree Type을 만들어 줍니다.
2 : BinaryTreeNode의 AddNode라는 함수를 만들어서 Value를 넣도록 합니다.
2-1 : 현재 노드의 값보다 새로들어온 노드의 값이 작을 때 -> 왼쪽에 붙여 줍니다.
2-2 : 왼쪽에 있는 노드가 없으면 왼쪽에 추가해 줍니다.
2-3 : 왼쪽에 노드가 있는 경우 왼쪽 노드에 다시 AddNode()함수를 재귀호출해서 그 결과를 반환해 줍니다.
2-4 : 현재 노드의 값보다 새로들어온 노드의 값이 작지 않으면 -> 오른쪽에 붙여 줍니다.
2-5 : 마찬가지로 오른쪽에 값이 없으면 오른쪽에 추가해 줍니다.
2-6 : 오른쪽 노드가 있으면 오른쪽 노드에 AddNode()함수를 재귀호출해서 그 결과를 반환해 줍니다.
3 : Tree를 새로 만드는 함수. 처음 시작값을 받고, 새로 만들어진 BinaryTree를 반환시켜 줍니다.
이제 main.go로 넘어와서
main.go
package main
import (
"./dataStruct"
)
func main() {
tree := dataStruct.NewBinaryTree(5) // 1
tree.Root.AddNode(3) // 2
tree.Root.AddNode(2)
tree.Root.AddNode(4)
tree.Root.AddNode(8)
tree.Root.AddNode(7)
tree.Root.AddNode(6)
tree.Root.AddNode(10)
tree.Root.AddNode(9)
tree.Print() // 3
}1 : 처음 RootNode가 5인 BinaryTree를 생성한 뒤
2 : 값을 넣어 줍니다.
3 : 출력하는 함수가 있다고 가정하고 호출한 뒤 binaryTree.go에서 만들어보죠!
binaryTree.go
func (t *BinaryTree) Print() { // 1
q := []*BinaryTreeNode{} // 2
q = append(q, t.Root) // 3
currentDepth := 0
for len(q) > 0 { // 4
var first depthNode // 1
first, q = q[0], q[1:] // 2
}
}1 : 출력을 위한 Print함수를 생성해 줍니다.
이 때 BFS를 사용해서 출력을 할 것입니다.
2 : BFS는 큐(Queue)를 사용하므로 먼저 큐를 생성해 줍니다.
3 : 큐에 Push 합니다.
4 : 큐가 비어있지 않았으면 for문을 돕니다.
4-1 : 첫번째 노드를 저장할 변수를 선언 합니다.
4-2 : 첫번째 노드와 큐를 갱신시켜 줍니다.
출력 값을 보게 되면

출력이 뭔가 이상하게 되어 있는 것을 확인 할 수 있죠.
이 부분은 binaryTree.go에서 add할 때 first는 큐의 첫번째 값이고, q값은 큐를 첫번째의 값을 뺀 값을 넣어주어야 하므로 두번째 부터 넣어 줍니다.
그 다음 현재 노드를 집어넣어야 하는데 현재 나온 노드가 몇번째 층에 나온 노드인지 알기 위해서 코드를 수정해 줍니다. binaryTree.go
type depthNode struct { // 1
depth int
node *BinaryTreeNode
}
func (t *BinaryTree) Print() { // 2
q := []depthNode{} // 1
q = append(q, depthNode{depth: 0, node: t.Root}) // 2
currentDepth := 0 // 3
for len(q) > 0 {
var first depthNode
first, q = q[0], q[1:]
if first.depth != currentDepth { // 4
fmt.Println() // 5
currentDepth = first.depth
}
fmt.Print(first.node.Val, " ") // 6
if first.node.left != nil { // 7
q = append(q, depthNode{depth: currentDepth + 1, node: first.node.left})
}
if first.node.right != nil { // 8
q = append(q, depthNode{depth: currentDepth + 1, node: first.node.right})
}
}
}1 : 깊이와 노드를 같이 가지고 있는 struct를 만들어 줍니다.
2-1 : 그리고 이 struct를 가지는 슬라이스를 만들어주고,
2-2 : Push할 때 처음의 depth는 0, node는 Rootnode를 넣어 줍니다.
2-3 : 현재 Depth를 표시하는 변수 입니다.
2-4 : first와 현재 depth가 다르면
2-5 : 한 줄을 띄워주고, currentDepth를 first.depth로 바꾸어주고,
2-6 : 값을 출력시켜 줍니다.
2-7 : left가 있다면 큐의 맨 뒤에 집어 넣어 줍니다.
큐에 집어 넣을 때 depth는 현재 depth의 1 더한 값(자식 노드니까)을 넣어주고, node는 first.node.left를 넣어주고,
2-8 : right가 있다면
큐에 집어 넣을 때 depth는 현재 depth의 1 더한 값(자식 노드니까)을 넣어주고, node는 first.node.right를 넣어줍니다.
func (n *BinaryTreeNode) AddNode(v int) *BinaryTreeNode {
// 현재 값이 새로 들어온 값 보다 작으면
if n.Val < v {
if n.left == nil {
n.left = &BinaryTreeNode{Val: v}
return n.left
} else {
return n.left.AddNode(v)
}
} else {
if n.right == nil {
n.right = &BinaryTreeNode{Val: v}
return n.right
} else {
return n.right.AddNode(v)
}
}
}이 부분에서 문제가 생긴건데 현재 값이 새로 들어온 값 보다 작을 때 오른쪽에 넣어야 되는데 왼쪽에 넣었습니다.
그래서 현재값이 더 큰 경우, 새로 들어온 값이 작은경우에 왼쪽에 넣을 수 있도록 아래와 같이 바꾸어 줍니다.
func (n *BinaryTreeNode) AddNode(v int) *BinaryTreeNode {
// 현재 값이 새로 들어온 값 보다 작으면
if n.Val > v {
if n.left == nil {
n.left = &BinaryTreeNode{Val: v}
return n.left
} else {
return n.left.AddNode(v)
}
} else {
if n.right == nil {
n.right = &BinaryTreeNode{Val: v}
return n.right
} else {
return n.right.AddNode(v)
}
}
}그러면 아래와 같이 정상적으로 바뀐 것을 알 수 있습니다.

이번에는 실제로 검색하는 것을 만들어보죠! main.go
package main
import (
"fmt"
"./dataStruct"
)
func main() {
tree := dataStruct.NewBinaryTree(5)
tree.Root.AddNode(3)
tree.Root.AddNode(2)
tree.Root.AddNode(4)
tree.Root.AddNode(8)
tree.Root.AddNode(7)
tree.Root.AddNode(6)
tree.Root.AddNode(10)
tree.Root.AddNode(9)
tree.Print()
if tree.Search(6) {
fmt.Println("found 6")
} else {
fmt.Println("Not found 6")
}
}main 함수에 이렇게 추가해주고, 트리 안에 6을 찾도록 해보죠!
그 후 binaryTree.go로 와서 Search함수를 추가해 줍니다!
func (t *BinaryTree) Search(v int) bool { // 1
return t.Root.Search(v)
}
func (n *BinaryTreeNode) Search(v int) bool { // 2
if n.Val == v { // 3
return true
} else if n.Val > v { // 4
if n.left != nil {
return n.left.Search(v)
}
return false // 5
} else {
if n.right != nil { // 6
return n.right.Search(v)
}
return false // 7
}
}
1 : Binary Tree의 함수입니다. 찾아야 되는 값 v를 받고, 반환값으로 bool형으로 합니다.
그리고 tree의 Root의 Search라는 함수를 호출 하도록 해줍니다.
2 : 그런데 Root에 Search라는 함수가 없기 때문에 만들어 줍니다.
이번에는 BinaryTreeNode의 Search함수를 만들어 줍니다.
3 : 내가 찾아야 되는 값과 현재 노드와의 값이 같은 경우 True를 return 시켜주고,
4 : 같지 않고, 내 값이 찾아야 되는 값보다 큰 경우 왼쪽에 있을 가능성이 높으므로 왼쪽 노드에서 Search하도록 해주고,
5 : 없는 경우인데 없다는 얘기는 나보다 작은 수가 없다는 의미 이므로 false를 return 시켜 줍니다.
6 : 오른쪽 노드가 있으면 오른쪽에 찾아보고,
7 : 오른쪽에도 없으면 나보다 큰 값이 없는 것이므로 이 경우도 없는 수가 되어 false를 return 시켜 줍니다.
이렇게 Search 함수가 만들어졌고, 제대로 찾는지 확인해보죠!
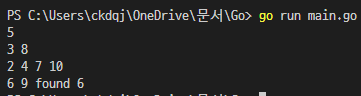
이번에는 찾았는지 여부만 반환하는게 아니라 몇번만에 찾았는지도 반환시켜보죠! main.go
func main() {
tree := dataStruct.NewBinaryTree(5)
tree.Root.AddNode(3)
tree.Root.AddNode(2)
tree.Root.AddNode(4)
tree.Root.AddNode(8)
tree.Root.AddNode(7)
tree.Root.AddNode(6)
tree.Root.AddNode(10)
tree.Root.AddNode(9)
tree.Print()
if found, cnt := tree.Search(6); found { // 1
fmt.Println("found 6")
} else {
fmt.Println("Not found 6")
}
}1 : 이 부분을 초기문이라고 해서 Search()를 먼저 실행하고, 그 결과를 found와 cnt에 대입하는 것이고, found가 true인 경우 fmt.Println("found 6")를 출력시킨다는 의미 입니다.
그 후 binaryTree.go로 와서 수정시켜보죠!
func (t *BinaryTree) Search(v int) (bool, int) {
return t.Root.Search(v, 1)
}
func (n *BinaryTreeNode) Search(v int, cnt int) (bool, int) {
if n.Val == v {
return true, cnt
} else if n.Val > v {
if n.left != nil {
return n.left.Search(v, cnt+1)
}
return false, cnt
} else {
if n.right != nil {
return n.right.Search(v, cnt+1)
}
return false, cnt
}
}이렇게 BinaryTree의 Search엔 초기값이기 때문에 cnt를 1 넣어주어 반환 하도록 하고, BinaryTreeNode의 Search엔 cnt를 입력받아 bool과 cnt를 return하도록 수정해 줍니다.
이제 main.go로 넘어와 cnt도 출력할 수 있게 수정해준 뒤 실행시켜 줍니다.
func main() {
tree := dataStruct.NewBinaryTree(5)
tree.Root.AddNode(3)
tree.Root.AddNode(2)
tree.Root.AddNode(4)
tree.Root.AddNode(8)
tree.Root.AddNode(7)
tree.Root.AddNode(6)
tree.Root.AddNode(10)
tree.Root.AddNode(9)
tree.Print()
if found, cnt := tree.Search(6); found {
fmt.Println("found 6 cnt : ", cnt)
} else {
fmt.Println("Not found 6 cnt : ", cnt)
}
}
이번에는 없는 숫자를 찾아보죠.
func main() {
tree := dataStruct.NewBinaryTree(5)
tree.Root.AddNode(3)
tree.Root.AddNode(2)
tree.Root.AddNode(4)
tree.Root.AddNode(8)
tree.Root.AddNode(7)
tree.Root.AddNode(6)
tree.Root.AddNode(10)
tree.Root.AddNode(9)
tree.Print()
if found, cnt := tree.Search(6); found {
fmt.Println("found 6 cnt : ", cnt)
} else {
fmt.Println("Not found 6 cnt : ", cnt)
}
if found, cnt := tree.Search(12); found {
fmt.Println("found 12 cnt : ", cnt)
} else {
fmt.Println("Not found 12 cnt : ", cnt)
}
}정상적으로 출력되는 것을 알 수 있습니다.
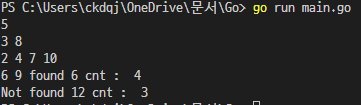
이진검색트리를 사용하는 이유는 검색을 빨리하기 위해서 입니다.
여기서의 검색은 많은 용도로 사용합니다. 예를 들면 회원가입 시 ID를 입력할 때 ID를 DataBase에 저장해야 하는데 이걸 저장할 때
ID의 가 ABCD라고 할 때 문자열을 비교하는건 까다롭기 때문에 문자열을 HASH처리해서 숫자로 만들거나 회원가입 순서로 번호를 지정할 수 있는데, 그 번호를 이진트리 같은 곳에 넣고 그 아이디에 해당하는 값이 있는지 확인하는데 이 때 처음부터 끝까지 찾는거 보단 빠르기 때문에 이진트리 검색을 사용합니다.
최종 코드
main.go
package main
import (
"fmt"
"./dataStruct"
)
func main() {
tree := dataStruct.NewBinaryTree(5)
tree.Root.AddNode(3)
tree.Root.AddNode(2)
tree.Root.AddNode(4)
tree.Root.AddNode(8)
tree.Root.AddNode(7)
tree.Root.AddNode(6)
tree.Root.AddNode(10)
tree.Root.AddNode(9)
tree.Print()
fmt.Println()
if found, cnt := tree.Search(6); found {
fmt.Println("found 6 cnt : ", cnt)
} else {
fmt.Println("Not found 6 cnt : ", cnt)
}
if found, cnt := tree.Search(12); found {
fmt.Println("found 12 cnt : ", cnt)
} else {
fmt.Println("Not found 12 cnt : ", cnt)
}
}binaryTree.go
package dataStruct
import "fmt"
type BinaryTreeNode struct {
Val int
left *BinaryTreeNode
right *BinaryTreeNode
}
type BinaryTree struct {
Root *BinaryTreeNode
}
func NewBinaryTree(v int) *BinaryTree {
tree := &BinaryTree{}
tree.Root = &BinaryTreeNode{Val: v}
return tree
}
func (n *BinaryTreeNode) AddNode(v int) *BinaryTreeNode {
if n.Val > v {
if n.left == nil {
n.left = &BinaryTreeNode{Val: v}
return n.left
} else {
return n.left.AddNode(v)
}
} else {
if n.right == nil {
n.right = &BinaryTreeNode{Val: v}
return n.right
} else {
return n.right.AddNode(v)
}
}
}
type depthNode struct {
depth int
node *BinaryTreeNode
}
func (t *BinaryTree) Print() {
q := []depthNode{}
q = append(q, depthNode{depth: 0, node: t.Root})
currentDepth := 0
for len(q) > 0 {
var first depthNode
first, q = q[0], q[1:]
if first.depth != currentDepth {
fmt.Println()
currentDepth = first.depth
}
fmt.Print(first.node.Val, " ")
if first.node.left != nil {
q = append(q, depthNode{depth: currentDepth + 1, node: first.node.left})
}
if first.node.right != nil {
q = append(q, depthNode{depth: currentDepth + 1, node: first.node.right})
}
}
}
func (t *BinaryTree) Search(v int) (bool, int) {
return t.Root.Search(v, 1)
}
func (n *BinaryTreeNode) Search(v int, cnt int) (bool, int) {
if n.Val == v {
return true, cnt
} else if n.Val > v {
if n.left != nil {
return n.left.Search(v, cnt+1)
}
return false, cnt
} else {
if n.right != nil {
return n.right.Search(v, cnt+1)
}
return false, cnt
}
}'프로그래밍(Basic) > Golang' 카테고리의 다른 글
| [바미] Go - Heap에 대해 알아보자2! (0) | 2021.02.01 |
|---|---|
| [바미] Go - Heap에 대해 알아보자! (0) | 2021.02.01 |
| [바미] Go - Tree BFS 와 Dijkstra에 대해 알아보자! (0) | 2021.01.26 |
| [바미] Go - Tree에 대해 알아보자! (0) | 2021.01.18 |
| [바미] Go - Packaging 과 Stack, Queue에 대해 알아보자! (0) | 2021.01.12 |