선형성(Linearity)
선형성이란 가산성과 동차성 성질을 동시에 만족하는 것을 말합니다.
가산성 (Additivity)
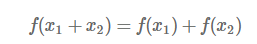
각각의 입력에 대한 결과를 합한 것과 입력을 합쳐서 넣은 결과가 동일하다.
이것이 가산성이고 superposition(중첩)이 가능하다고 한다.
다시 말해 복잡한 입력 x1 + x2에 대한 결과를 알기 어려울 때 이미 잘 알고 있거나 계산하기 쉬운 단순한 입력 x1과 x2를
이용해 각각의 결과를 얻고 단순히 합하기만 하면 되는 것을 말합니다.
동차성 (Homogeneity)
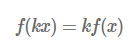
입력을 몇 배 늘리거나 줄였을 때 그 결과도 입력이 조정된 비율만큼 조정되는 성질을 말합니다.
선형성이 중요한 이유
예를 들어 어떤 선형적으로 거동하는 물체를 1N의 힘으로 눌렀을 때 1mm만큼 변형하고 2N의 힘으로 눌렀을 때 2mm만큼 변형한다고 가정해보죠.
이 물체에 먼저 2N의 힘을 주고 다시 그대로 1N의 힘을 추가할 때 이 물체는 선형적으로 거동하기 때문에 먼저 2mm만큼 변형하고
추가로 1mm만큼 더 변형해 총 3mm만큼 변형할 것이라고 예상할 수 있겠죠?
이것을 가산성이라 부릅니다. 이것은 물체에 3N의 힘이 가해졌을 때 3 mm만큼 변형하는 것과 같죠.
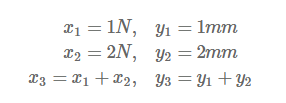
다시 위의 어떤 선형적으로 거동하는 물체를 1N의 힘으로 눌렀을 때를 생각해보죠. 위의 글이 이해가 되셨다면 이 물체는 1mm만큼 변형한다는 것을 알고 있을겁니다.
이 물체가 선형적으로 거동한다면 3N의 힘으로 눌렀을 때 1N일 때의 변형의 세 배만큼 변형할 것인데 이것을 동차성이라 부릅니다.
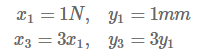
이 물체는 가산성과 동차성을 모두 만족하므로 선형성을 만족하는 물체라고 할 수 있습니다.
이와 같이 우리가 만든 어떤 수학 모델이 선형이라면 계산도 쉬워지고 결과의 예측이 쉬워지게 됩니다.
만약 모델이 비선형성을 가지고 있다면 우리는 단순하게 선형대수학을 이용해 계산을 할 수 없게 되고 Newton-Rhapson method와
같은 알고리즘을 이용해 점진적으로 해를 찾아나가야 합니다. (물론 오차 범위 안에서 그 해가 맞을 거라고 수용할 뿐이죠.)
선형 상미분방정식으로 어떤 물리 현상을 표현할 수 있을 때 우리는 선형성을 이용하여 쉽게 정확한 해를 구하고 결과를 예측할 수 있
습니다.
만약 유체역학과 같이 비선형 방정식의 대표주자인 나비에-스톡스 방정식을 풀어야 하는 경우에는 전적으로 컴퓨터에 의존하여 예측할 수밖에 없습니다.
선형이 아닌 경우
아래 방정식은 선형일까요?
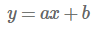
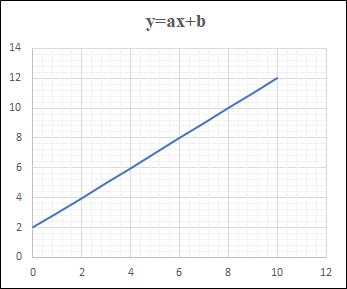
성급하게 답하기 전에 선형성의 두 가지 조건인 가산성과 동차성을 만족하는지 하나하나 따져봅시다.
우선 입력 x1, x2에 대해 출력 y1, y2를 갖는다고 해보죠.
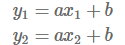
가산성은 아래와 같게 됩니다.
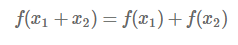
먼저 좌변을 생각해보면 아래와 같습니다.
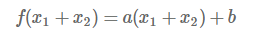
다음 우변을 생각해 보면 아래와 같습니다.
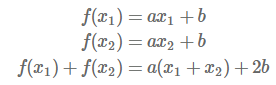
좌변과 우변이 일치하지 않으므로 가산성에 위배되게 됩니다.
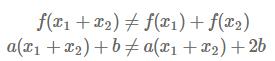
동차성은 아래와 같습니다.
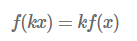
위 방정식에 적용해 보면 좌변은 아래와 같습니다.
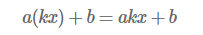
이것은 동차성에 위배된다는 것을 알 수 있죠.
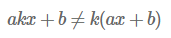
따라서 이 방정식은 선형이 아닙니다. 선형이려면 상수 b가 없어야 하죠. 선형인 것 같지만 선형이 아닌 대표적인 예 중 하나 입니다.
참고
- http://www.ktword.co.kr/test/view/view.php?m_temp1=6336
- https://ko.wikipedia.org/wiki/%EC%84%A0%ED%98%95%EC%84%B1
'프로그래밍(Basic) > 이론' 카테고리의 다른 글
| [바미] Object, Class, Instance. (0) | 2022.12.27 |
|---|---|
| [바미] Java - Garbage Collection (0) | 2022.12.06 |
| [바미] BROWSER-RENDERING에 대하여 (0) | 2022.08.30 |
| [바미] REST API에 대하여 (0) | 2022.08.18 |
| [바미] Deadlock의 해결방안 (0) | 2022.08.16 |