트리(Tree)?
계층적인 구조를 나타내는 자료구조입니다.
트리는 루트 노드(root node)에서 시작하여 각 노드가 0개 이상의 자식 노드(child node)를 가지며, 자식 노드들도 다시 트리 구조를 형성하는 형태로 이루어져 있습니다.
트리의 구조

- 루트 노드(root node): 부모가 없는 최상위 노드. 트리는 하나의 루트 노드만을 가집니다.
- 단말 노드(leaf node): 자식 노드가 없는 노드. '말단 노드' 또는 '잎 노드'라고도 부릅니다.
- 내부 노드(internal node): 단말 노드가 아닌 노드를 의미합니다.
- 간선(edge): 노드 간을 연결하는 선으로, 링크(link) 또는 브랜치(branch)라고도 부릅니다.
- 형제 노드(sibling): 같은 부모를 가지는 노드들을 의미합니다.
- 노드의 크기(size): 자신을 포함한 모든 자손 노드의 개수를 의미합니다.
- 노드의 깊이(depth): 루트 노드에서 특정 노드에 도달하기 위해 거쳐야 하는 간선의 수를 의미합니다.
- 노드의 레벨(level): 트리의 특정 깊이를 가지는 노드들의 집합을 의미합니다.
- 노드의 차수(degree): 각 노드가 지닌 자식 노드(하위 트리)의 개수를 의미합니다.
- 트리의 차수(degree of tree): 트리 내에서 가장 큰 노드의 차수를 의미합니다.
- 트리의 높이(height): 루트 노드에서 가장 깊숙한 노드의 깊이를 의미합니다.
트리의 종류
트리는 크게 일반 트리와 이진 트리로 나뉩니다.
일반 트리 (General Tree)는 각 노드가 임의의 수의 자식 노드를 가질 수 있는 트리이고,
이진 트리 (Binary Tree)는 각 노드가 최대 두 개의 자식 노드를 가지는 트리입니다.
이진 트리 중에서 균형 이진 트리 (Balanced Binary Tree)라는 것이 있는데 모든 리프 노드가 루트로부터 동일한 거리에 있거나, 거리가 1만큼 차이 나는 트리입니다. 대표적으로 AVL 트리와 레드-블랙 트리가 있죠.
트리의 탐색 방법
트리의 깊이 우선 탐색(DFS)에는 전위 순회, 중위 순회, 후위 순회 방법이 있습니다.
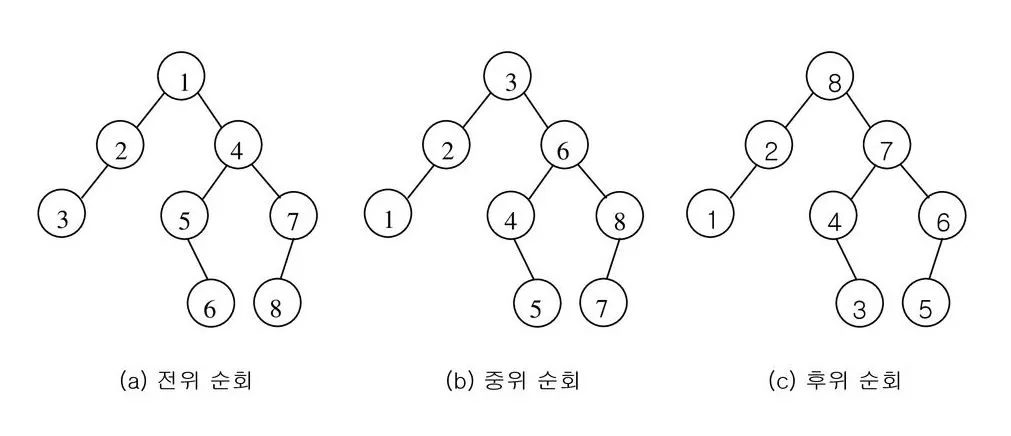
전위 순회 (preorder traverse)
현재 노드를 먼저 방문한 후, 왼쪽 자식 노드와 오른쪽 자식 노드를 순서대로 방문하는 방법입니다.
따라서 진행순서는 현재 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드 순으로 진행됩니다.
루트 노드를 가장 먼저 방문하는 게 특징이고, 트리 구조를 복사하거나, 복잡한 표현식을 계산하는 데 유용합니다.
중위 순회(Inorder Traversal)
왼쪽 자식 노드를 먼저 방문한 후, 현재 노드를 방문하고, 마지막으로 오른쪽 자식 노드를 방문하는 방법입니다.
따라서 진행순서는 왼쪽 자식 노드 -> 현재 노드 -> 오른쪽 자식 노드 순으로 진행됩니다.

이진 탐색 트리에서 중위 순회를 하면 노드의 값이 오름차순으로 정렬되는데 수학적인 표현식을 계산하거나, 정렬된 순서로 데이터에 접근할 때 유용합니다.
후위 순회 (Postorder Traversal)
왼쪽 자식 노드와 오른쪽 자식 노드를 먼저 방문한 후, 현재 노드를 방문하는 방법입니다.
따라서 진행 순서는 왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 현재 노드 순으로 진행됩니다.

리프 노드를 가장 먼저 방문하는 게 특징이고, 트리의 구조를 삭제하거나, 후위 표기법을 계산하는 데 유용합니다.
코드(Java)
이제 실제로 구현 해보도록 하겠습니다. 이번 예시는 밸런스 트리(B-트리)와 이진 트리를 구현하는 예제입니다.
package example_5;
// B-트리 노드 정의
class BTreeNode {
int[] keys; // 키 배열
int t; // 최소 차수
BTreeNode[] C; // 자식 노드 배열
int n; // 현재 키의 수
boolean leaf; // 리프 노드 여부
// B-트리 노드 생성자
public BTreeNode(int t, boolean leaf) {
this.t = t; // 최소 차수 설정
this.leaf = leaf; // 리프 노드 여부 설정
this.keys = new int[2 * t - 1]; // 키 배열 초기화
this.C = new BTreeNode[2 * t]; // 자식 노드 배열 초기화
this.n = 0; // 현재 키의 수 초기화
}
// 노드 순회
public void traverse() {
int i;
for (i = 0; i < this.n; i++) {
if (!this.leaf) {
this.C[i].traverse(); // 자식 노드 순회
}
System.out.print(" " + this.keys[i]); // 현재 키 출력
}
if (!this.leaf) {
this.C[i].traverse(); // 마지막 자식 노드 순회
}
}
// 키 검색
public BTreeNode search(int k) {
int i = 0;
while (i < n && k > keys[i]) {
i++;
}
if (keys[i] == k) {
return this; // 키를 찾으면 현재 노드 반환
}
if (leaf) {
return null; // 리프 노드인 경우 null 반환
}
return C[i].search(k); // 자식 노드에서 검색
}
// 비가득 노드에 키 삽입
public void insertNonFull(int k) {
int i = n - 1; // 현재 노드의 마지막 키 인덱스
// 노드가 리프 노드인 경우
if (leaf) {
// 새 키의 위치를 찾기 위해 키들을 한 칸씩 뒤로 이동
while (i >= 0 && keys[i] > k) {
keys[i + 1] = keys[i];
i--;
}
keys[i + 1] = k; // 새 키 삽입
n = n + 1; // 키의 개수 증가
} else {
// 새 키가 삽입될 자식 노드의 인덱스를 찾기 위해 반복
while (i >= 0 && keys[i] > k) {
i--;
}
// 찾은 자식 노드가 가득 찬 경우
if (C[i + 1].n == 2 * t - 1) {
splitChild(i + 1, C[i + 1]); // 자식 노드 분할
// 분할 후, 새 키가 어느 자식 노드로 갈지 결정
if (keys[i + 1] < k) {
i++;
}
}
// 적절한 자식 노드에 재귀적으로 삽입
C[i + 1].insertNonFull(k);
}
}
// 자식 노드 분할
public void splitChild(int i, BTreeNode y) {
// y의 t번째 자식 z 생성 (y와 같은 최소 차수와 리프 속성을 가짐)
BTreeNode z = new BTreeNode(y.t, y.leaf);
z.n = t - 1; // z의 키 개수는 t-1로 설정
// y의 뒤쪽 키를 z로 이동
for (int j = 0; j < t - 1; j++) {
z.keys[j] = y.keys[j + t];
}
// y가 리프 노드가 아니면, y의 자식도 z로 이동
if (!y.leaf) {
for (int j = 0; j < t; j++) {
z.C[j] = y.C[j + t];
}
}
y.n = t - 1; // y의 키 개수를 t-1로 감소
// y의 자식들을 한 칸씩 뒤로 이동
for (int j = n; j >= i + 1; j--) {
C[j + 1] = C[j];
}
// 새로운 자식 z를 y의 다음 자식으로 설정
C[i + 1] = z;
// y의 키들을 한 칸씩 뒤로 이동
for (int j = n - 1; j >= i; j--) {
keys[j + 1] = keys[j];
}
// y의 중간 키를 부모 노드로 이동
keys[i] = y.keys[t - 1];
n = n + 1; // 부모 노드의 키 개수 증가
}
}
// B-트리 정의
class BTree {
BTreeNode root; // 루트 노드
int t; // 최소 차수
// B-트리 생성자
public BTree(int t) {
this.root = null; // 루트 노드 초기화
this.t = t; // 최소 차수 설정
}
// 트리 순회
public void traverse() {
if (root != null) {
root.traverse(); // 루트 노드 순회
}
}
// 키 검색
public BTreeNode search(int k) {
return root == null ? null : root.search(k); // 루트 노드에서 검색
}
// 키 삽입
public void insert(int k) {
// 트리가 비어 있으면 새로운 루트 노드 생성
if (root == null) {
root = new BTreeNode(t, true); // 새로운 루트 노드 생성 (리프 노드)
root.keys[0] = k; // 첫 키 삽입
root.n = 1; // 루트 노드의 키 개수 설정
} else {
// 루트 노드가 가득 차면 새로운 루트 노드 생성
if (root.n == 2 * t - 1) {
BTreeNode s = new BTreeNode(t, false); // 새로운 비리프 루트 노드 생성
s.C[0] = root; // 새로운 루트의 첫 자식으로 기존 루트 설정
s.splitChild(0, root); // 기존 루트 분할
int i = 0;
if (s.keys[0] < k) { // 새로운 키의 위치 결정
i++;
}
s.C[i].insertNonFull(k); // 적절한 자식 노드에 키 삽입
root = s; // 새로운 루트를 현재 루트로 설정
} else {
root.insertNonFull(k); // 루트 노드에 직접 키 삽입
}
}
}
}
// 이진 트리 노드 정의
class BinaryTreeNode {
int data; // 노드 데이터
BinaryTreeNode left, right; // 왼쪽 및 오른쪽 자식
public BinaryTreeNode(int item) {
data = item;
left = right = null; // 자식 노드 초기화
}
}
// 이진 트리 정의
class BinaryTree {
BinaryTreeNode root; // 루트 노드
public BinaryTree() {
root = null; // 루트 노드 초기화
}
void insert(int key) {
root = insertRec(root, key); // 재귀적으로 키 삽입
}
BinaryTreeNode insertRec(BinaryTreeNode root, int key) {
if (root == null) {
root = new BinaryTreeNode(key); // 새로운 노드 생성
return root;
}
if (key < root.data)
root.left = insertRec(root.left, key); // 왼쪽 자식에 삽입
else if (key > root.data)
root.right = insertRec(root.right, key); // 오른쪽 자식에 삽입
return root;
}
void inorder() {
inorderRec(root); // 중위 순회
}
void inorderRec(BinaryTreeNode root) {
if (root != null) {
inorderRec(root.left); // 왼쪽 자식 순회
System.out.print(root.data + " "); // 현재 노드 데이터 출력
inorderRec(root.right); // 오른쪽 자식 순회
}
}
}
// 메인 클래스
public class Main {
public static void main(String[] args) {
// 이진 트리 생성 및 삽입
BinaryTree binaryTree = new BinaryTree();
binaryTree.insert(50);
binaryTree.insert(30);
binaryTree.insert(20);
binaryTree.insert(40);
binaryTree.insert(70);
binaryTree.insert(60);
binaryTree.insert(80);
System.out.print("Binary Tree In-order traversal: ");
binaryTree.inorder(); // 이진 트리 중위 순회
System.out.println();
// B-트리 생성 및 삽입
int t = 3; // B-트리의 최소 차수
BTree bTree = new BTree(t);
bTree.insert(10);
bTree.insert(20);
bTree.insert(5);
bTree.insert(6);
bTree.insert(12);
bTree.insert(30);
bTree.insert(7);
bTree.insert(17);
System.out.print("B-Tree traversal: ");
bTree.traverse(); // B-트리 순회
System.out.println();
}
}코드 설명
먼저 BTreeNode 클래스, BTree 클래스, BinaryTreeNode 클래스, BinaryTree 클래스, Main 클래스로 나뉘어져 있습니다.
BTreeNode 클래스
BTreeNode 클래스는 B-트리의 노드를 정의하는 클래스입니다.
이 클래스에서는 각 노드에 저장될 키, 자식 노드 배열, 키의 개수 및 노드가 리프인지 여부를 포함하고 있습니다.
class BTreeNode {
int[] keys; // 키 배열
int t; // 최소 차수
BTreeNode[] C; // 자식 노드 배열
int n; // 현재 키의 수
boolean leaf; // 리프 노드 여부용도에 맞게 각 변수를 선언했습니다. 변수에 대한 설명은 주석에 달았습니다.
생성자
// B-트리 노드 생성자
public BTreeNode(int t, boolean leaf) {
this.t = t; // 최소 차수 설정
this.leaf = leaf; // 리프 노드 여부 설정
this.keys = new int[2 * t - 1]; // 키 배열 초기화
this.C = new BTreeNode[2 * t]; // 자식 노드 배열 초기화
this.n = 0; // 현재 키의 수 초기화
}B-트리 노드의 생성자 부분입니다. 최소 차수와 리프 여부를 받아 노드를 초기화합니다. keys 배열과 C 배열도 초기화시켜줍니다.
각 메서드들
// 노드 순회
public void traverse() {
int i;
for (i = 0; i < this.n; i++) {
if (!this.leaf) {
this.C[i].traverse(); // 자식 노드 순회
}
System.out.print(" " + this.keys[i]); // 현재 키 출력
}
if (!this.leaf) {
this.C[i].traverse(); // 마지막 자식 노드 순회
}
}노드를 순회하며 모든 키를 출력하는 메서드 입니다. 재귀적으로 자식 노드도 순회하죠.
// 키 검색
public BTreeNode search(int k) {
int i = 0;
while (i < n && k > keys[i]) {
i++;
}
if (keys[i] == k) {
return this; // 키를 찾으면 현재 노드 반환
}
if (leaf) {
return null; // 리프 노드인 경우 null 반환
}
return C[i].search(k); // 자식 노드에서 검색
}노드에서 키 k를 검색하는 메서드 입니다. 키가 현재 노드에 있으면 그 노드를 반환하고, 리프 노드일 경우 null을 반환하며, 그렇지 않으면 자식 노드에서 재귀적으로 검색하는 형태죠.
// 비가득 노드에 키 삽입
public void insertNonFull(int k) {
int i = n - 1; // 현재 노드의 마지막 키 인덱스
// 노드가 리프 노드인 경우
if (leaf) {
// 새 키의 위치를 찾기 위해 키들을 한 칸씩 뒤로 이동
while (i >= 0 && keys[i] > k) {
keys[i + 1] = keys[i];
i--;
}
keys[i + 1] = k; // 새 키 삽입
n = n + 1; // 키의 개수 증가
} else {
// 새 키가 삽입될 자식 노드의 인덱스를 찾기 위해 반복
while (i >= 0 && keys[i] > k) {
i--;
}
// 찾은 자식 노드가 가득 찬 경우
if (C[i + 1].n == 2 * t - 1) {
splitChild(i + 1, C[i + 1]); // 자식 노드 분할
// 분할 후, 새 키가 어느 자식 노드로 갈지 결정
if (keys[i + 1] < k) {
i++;
}
}
// 적절한 자식 노드에 재귀적으로 삽입
C[i + 1].insertNonFull(k);
}
}현재 노드가 가득 차지 않았을 때 키를 삽입하는 메서드입니다. 삽입하려는 노드가 리프 노드인 지, 내부 노드인 지에 따라 동작하는 형태가 다른데 아래와 같습니다.
리프 노드인 경우
- 리프 노드에서는 키들을 한 칸씩 뒤로 이동시켜 새 키가 들어갈 자리를 만듭니다.
- 새 키를 삽입하고, 키의 개수를 증가시켜줍니다.
내부 노드인 경우
- 새 키가 삽입될 자식 노드의 인덱스를 찾습니다.
- 찾은 자식 노드가 가득 차면 해당 자식 노드를 분할합니다.
- 새 키가 어느 자식 노드로 갈지 결정한 후 적절한 자식 노드에 재귀적으로 삽입합니다.
// 자식 노드 분할
public void splitChild(int i, BTreeNode y) {
// y의 t번째 자식 z 생성 (y와 같은 최소 차수와 리프 속성을 가짐)
BTreeNode z = new BTreeNode(y.t, y.leaf);
z.n = t - 1; // z의 키 개수는 t-1로 설정
// y의 뒤쪽 키를 z로 이동
for (int j = 0; j < t - 1; j++) {
z.keys[j] = y.keys[j + t];
}
// y가 리프 노드가 아니면, y의 자식도 z로 이동
if (!y.leaf) {
for (int j = 0; j < t; j++) {
z.C[j] = y.C[j + t];
}
}
y.n = t - 1; // y의 키 개수를 t-1로 감소
// y의 자식들을 한 칸씩 뒤로 이동
for (int j = n; j >= i + 1; j--) {
C[j + 1] = C[j];
}
// 새로운 자식 z를 y의 다음 자식으로 설정
C[i + 1] = z;
// y의 키들을 한 칸씩 뒤로 이동
for (int j = n - 1; j >= i; j--) {
keys[j + 1] = keys[j];
}
// y의 중간 키를 부모 노드로 이동
keys[i] = y.keys[t - 1];
n = n + 1; // 부모 노드의 키 개수 증가
}
}가득 찬 자식 노드를 분할하는 메서드입니다. 자식 노드를 반으로 나누고, 중간 키를 부모 노드로 올려 균형을 유지하죠.
먼저 새로운 자식 노드 생성합니다. y의 t번째 자식 z를 생성합니다. y와 같은 최소 차수와 리프 속성을 가지며 이 때 z의 키 개수를 t-1로 설정해줍니다.
그 후 y의 뒤쪽 키를 z로 이동시켜주고, y가 리프 노드가 아닌 경우 y의 자식도 z로 이동시켜 준 뒤 y의 키 개수를 t-1로 감소시킵니다.
그 다음 y의 키 개수를 t-1로 감소시켜주고, 새로운 자식 z를 y의 다음 자식으로 지정해줍니다.
그 다음 y의 중간 키를 부모 노드로 이동시키고, 부모 노드의 키 개수를 증가시키는 형태로 균형을 유지하는 형태의 메서드입니다.
B-트리 클래스
최소 차수를 받아서 초기화되며, 키를 삽입하고 검색하고 트리를 순회하는 기능을 제공하는 클래스입니다.
필드 변수 생성
BTreeNode root; // 루트 노드
int t; // 최소 차수root 변수는 트리의 루트 노드를 가리키고, t 변수는 최소 차수를 의미하는데 각 노드는 최소 t개의 자식을 가져야 합니다.
B-Tree 생성
public BTree(int t) {
this.root = null; // 루트 노드 초기화
this.t = t; // 최소 차수 설정
}최소 차수를 받아서 B-트리를 초기화한 뒤, 루트 노드를 null로 초기화 해줍니다.
트리 순회 메서드
public void traverse() {
if (root != null) {
root.traverse(); // 루트 노드 순회
}
}트리 전체를 순회하여 모든 키를 출력해주는데 루트 노드가 null이 아니면 루트 노드부터 순회하도록 동작합니다.
키 검색 메서드
public BTreeNode search(int k) {
return root == null ? null : root.search(k); // 루트 노드에서 검색
}주어진 키 k를 트리에서 검색하는데 루트 노드가 null이면 null을 반환하고, 그렇지 않으면 루트 노드에서 검색을 시작하도록 만들었습니다.
키 삽입
public void insert(int k) {
// 트리가 비어 있으면 새로운 루트 노드 생성
if (root == null) {
root = new BTreeNode(t, true); // 새로운 루트 노드 생성 (리프 노드)
root.keys[0] = k; // 첫 키 삽입
root.n = 1; // 루트 노드의 키 개수 설정
} else {
// 루트 노드가 가득 차면 새로운 루트 노드 생성
if (root.n == 2 * t - 1) {
BTreeNode s = new BTreeNode(t, false); // 새로운 비리프 루트 노드 생성
s.C[0] = root; // 새로운 루트의 첫 자식으로 기존 루트 설정
s.splitChild(0, root); // 기존 루트 분할
int i = 0;
if (s.keys[0] < k) { // 새로운 키의 위치 결정
i++;
}
s.C[i].insertNonFull(k); // 적절한 자식 노드에 키 삽입
root = s; // 새로운 루트를 현재 루트로 설정
} else {
root.insertNonFull(k); // 루트 노드에 직접 키 삽입
}
}
}키 k를 트리에 삽입하는 메서드입니다. 각 조건에 따라 동작하는 형태가 다릅니다.
트리가 비어 있을 때 키를 삽입 할 때
- root가 null이면 새로운 루트 노드를 생성하고 키를 삽입합니다.
- 이 루트 노드는 리프 노드로 설정됩니다.
- 첫 키를 삽입하고 루트 노드의 키 개수를 1로 설정합니다.
루트 노드가 가득 찬 경우
- 루트 노드의 키 개수가 2 * t - 1이면 새로운 루트 노드를 생성합니다.
- 새로운 루트 노드는 비리프 노드로 설정됩니다.
- 기존 루트를 새로운 루트 노드의 첫 자식으로 설정하고, 기존 루트를 분할합니다.
- 분할 후, 새로운 키 k가 어느 자식 노드로 갈지 결정하고 삽입합니다.
- 새로운 루트를 현재 루트로 설정합니다.
루트 노드가 가득 차지 않은 경우
- 루트 노드에 직접 키를 삽입합니다.
- insertNonFull 메서드를 호출하여 비가득 노드에 키를 삽입합니다.
BTreeNode 클래스
B-Tree의 노드를 정의하는 클래스입니다.
각 노드는 키 배열, 자식 노드 배열, 현재 키의 수, 리프 노드 여부를 가지고 있습니다.
노드 생성자
class BTreeNode {
int[] keys; // 키 배열
int t; // 최소 차수
BTreeNode[] C; // 자식 노드 배열
int n; // 현재 키의 수
boolean leaf; // 리프 노드 여부
public BTreeNode(int t, boolean leaf) {
this.t = t; // 최소 차수 설정
this.leaf = leaf; // 리프 노드 여부 설정
this.keys = new int[2 * t - 1]; // 키 배열 초기화
this.C = new BTreeNode[2 * t]; // 자식 노드 배열 초기화
this.n = 0; // 현재 키의 수 초기화
}
}배열, 자식 노드 배열, 현재 키의 수, 리프 노드 여부를 초기화하여 노드를 생성합니다.
이진 트리 (Binary Tree) 클래스
이진 트리의 노드를 정의하는 클래스입니다. 각 노드는 데이터와 왼쪽 및 오른쪽 자식 노드를 가지죠.
생성자
class BinaryTree {
BinaryTreeNode root; // 루트 노드
public BinaryTree() {
root = null; // 루트 노드 초기화
}
}루트 노드를 초기화하여 BinaryTree를 생성해줍니다.
노드 삽입 메서드
void insert(int key) {
root = insertRec(root, key); // 재귀적으로 키 삽입
}
BinaryTreeNode insertRec(BinaryTreeNode root, int key) {
if (root == null) {
root = new BinaryTreeNode(key); // 새로운 노드 생성
return root;
}
if (key < root.data)
root.left = insertRec(root.left, key); // 왼쪽 자식에 삽입
else if (key > root.data)
root.right = insertRec(root.right, key); // 오른쪽 자식에 삽입
return root;
}주어진 키를 이진 트리에 삽입하는 메서드 입니다.
insertRec 메서드는 재귀적으로 노드를 삽입하는데 키가 루트보다 작으면 왼쪽 자식에, 크면 오른쪽 자식에 삽입하는 형태로 동작합니다.
중위 순회 메서드
void inorder() {
inorderRec(root); // 중위 순회
}
void inorderRec(BinaryTreeNode root) {
if (root != null) {
inorderRec(root.left); // 왼쪽 자식 순회
System.out.print(root.data + " "); // 현재 노드 데이터 출력
inorderRec(root.right); // 오른쪽 자식 순회
}
}inorder 메서드는 inorderRec 메서드를 호출하여 재귀적으로 왼쪽 자식, 현재 노드, 오른쪽 자식 순으로 순회 트리를 중위 순회하며 데이터를 출력하는 형태로 동작하는 메서드 입니다.
메인 클래스(Main)
이제 메인 클래스 부분입니다. B-트리와 이진 트리를 생성하고, 삽입하는 부분입니다.
이진 트리 생성, 삽입
public class Main {
public static void main(String[] args) {
// 이진 트리 생성 및 삽입
BinaryTree binaryTree = new BinaryTree();
binaryTree.insert(50);
binaryTree.insert(30);
binaryTree.insert(20);
binaryTree.insert(40);
binaryTree.insert(70);
binaryTree.insert(60);
binaryTree.insert(80);
System.out.print("Binary Tree In-order traversal: ");
binaryTree.inorder(); // 이진 트리 중위 순회
System.out.println();이진 트리를 생성하고, 여러 키를 삽입한 후 중위 순회를 통해 트리를 출력해줍니다.
B-트리 생성, 삽입
int t = 3; // B-트리의 최소 차수
BTree bTree = new BTree(t);
bTree.insert(10);
bTree.insert(20);
bTree.insert(5);
bTree.insert(6);
bTree.insert(12);
bTree.insert(30);
bTree.insert(7);
bTree.insert(17);
System.out.print("B-Tree traversal: ");
bTree.traverse(); // B-트리 순회
System.out.println();B-트리를 생성하고, 여러 키를 삽입한 후 트리를 순회하여 출력 해줍니다.
'프로그래밍(Basic) > 이론' 카테고리의 다른 글
| [바미] 큐잉 이론(Queueing Theory)이란? (0) | 2024.12.09 |
|---|---|
| [바미] 자료구조 - 해시맵(HashMap) (0) | 2024.07.19 |
| [바미] 자료구조 - 그래프(Graph) (0) | 2024.07.12 |
| [바미] 자료구조 - 큐(Queue) (0) | 2024.07.11 |
| [바미] 자료구조 - 스택(Stack) (0) | 2024.07.09 |