[바미] Go - Heap 을 이용하여 문제를 풀어보자!

매일프로그래밍 이라는 곳에서 나왔던 문제를 풀어보려 합니다.

문제는 아래와 같습니다.

 

문제) 정수 배열(int array)과 정수 N이 주어지면, N번째로 큰 배열 원소를 찾으시오.

예제)

Input : [-1, 3, -1, 5, 4], 2
Output : 4

 

Input : [2, 4, -2, -3, 8], 1
Output : 8

 

Input : [-5, 3, 1], 3
Output : -5

 

이 문제를 푸는 방법은 여러가지가 있겠지만

Input : [-1, 3, -1, 5, 4], 2
Output : 4

의 경우 가장 무식하게, 단순하게 푸는 방법은 배열 2개 짜리를 하나 만들고, 가장 큰 값을 앞에, 두번째로 큰 값을 뒤에 적어주는 방법입니다.

 

그래서 처음에 -1이 나왔고, 3이 있는데 3과 -1을 비교 했을 때 3이 크므로 3을 앞에 넣고, -1을 뒤에 넣어 줍니다.

3

-1

그 다음 3과 -1은 같으니까 건너 뛰고, 5는 3보다 크므로 5를 앞에 넣고, 3을 뒤로 보내 줍니다.

5

3

그 다음 4는 5보다는 작고 3보다는 크므로 3이랑 바꿉니다.

5

3

그렇게 해서 4가 나오게 됩니다. 하지만 이 경우의 문제는 원소가 매우 큰 경우에 문제가 되죠.

만약 1억개의 원소가 있고 이 중에서 2만 5천 번째 큰 수를 구하라고 했을 때 방금 풀었던 형태로 풀게 되면 2만 5천개의 배열이 있고, 1억개의 원소가 있을 때 2만 5천개의 배열은 큰 수 부터 2만 5천개가 정렬되어 있을 것이고, 2만 5천 1번째부터 그 수가 배열에 들어갈지 여부를 확인하려면 2만 5천개의 배열을 처음부터 끝까지 다 비교를 해야 합니다.

그 다음수도 마찬가지 일 것 입니다. 그 때 1억 * 2만 5천번의 for문을 돌려야 합니다.

이 때 N(배열의 갯수) * M(몇번째인지 나타내는 것)알고리즘이라고 합니다.

N과 M이 작으면 문제가 되지 않지만 크면 문제가 됩니다.

 

두번째 방법은

Input : [-1, 3, -1, 5, 4], 2
Output : 4

이렇게 있을 때 위의 배열을 큰 수 부터 정렬을 시켜줍니다.

그 다음에 2번째 수를 반환하는 것이죠.

이 방법의 속도를 알아보자. 정렬은 RADIX Sort와 Heap Sort방법이 있다고 말했는데 RADIX Sort는 가장 빠른 정렬방법이지만 일반적인 경우엔 사용할 수 없습니다. 물론 이 정렬이 RADIX Sort방법을 사용할 수 있으면 사용하면 되지만 일반적인 경우엔 사용할 수 없습니다.

 

그래서 다른 정렬을 사용해야 하는데 Heap Sort, Quick Sort, Merge Sort, Insert Sort를 사용해야 하는데 모두 Nlog2^N이 듭니다.

N은 배열의 갯수이고 log2^N만큼 속도가 필요하죠.

그래프로 설명하자면 아래와 같은데

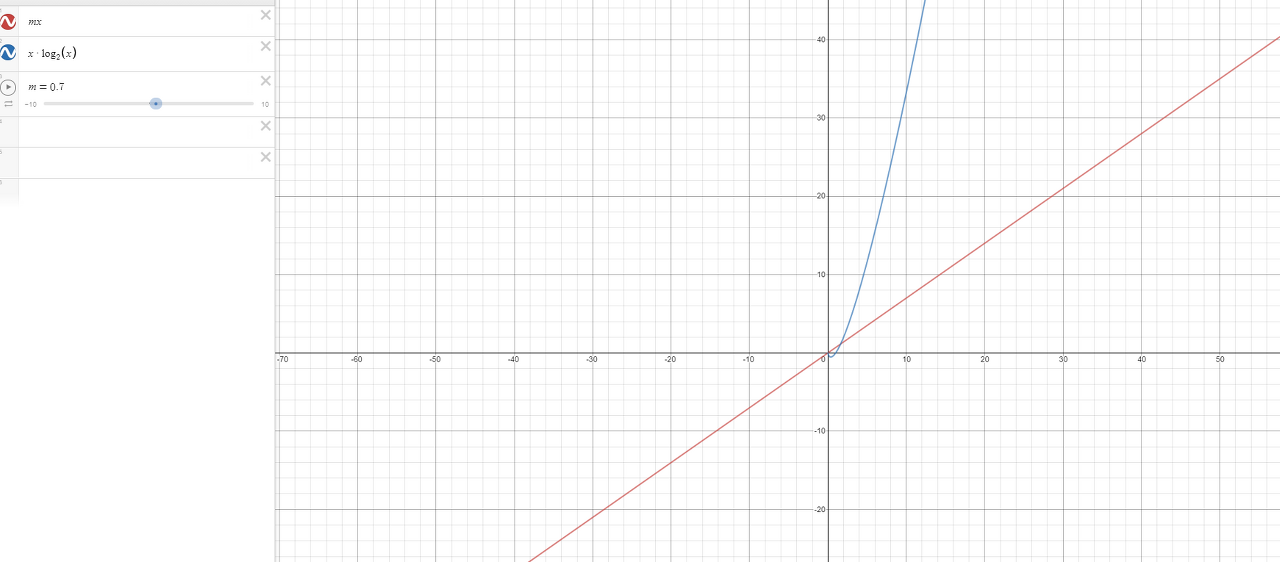
첫번째 파란색 그래프 mx라는 것은 첫번째 방법을 의미합니다. (여기선 n대신 x를 넣었습니다.)

x가 늘어날 때 마다 속도가 비례해서 늘어납니다.

두번째 주황색 그래프는 정렬시킨 다음에 정렬된 배열에서 원하는 번째 수를 가져오는 방법입니다.
y축이 속도, x축이 항목 갯수인데 보게 되면 항목갯수가 늘어날 때 파란색 선이 더 빨리 끝나는 것을 알 수 있습니다.

 

그런데 여기서 m의 값을 0.7이라고 가정한것인데 m을 1로 줘서 살펴보죠.

 

항목이 2일 때는 서로 같지만 x가 늘어날 경우에 2번째 방법이 더 오래 걸리는 것을 알 수 있습니다.

 

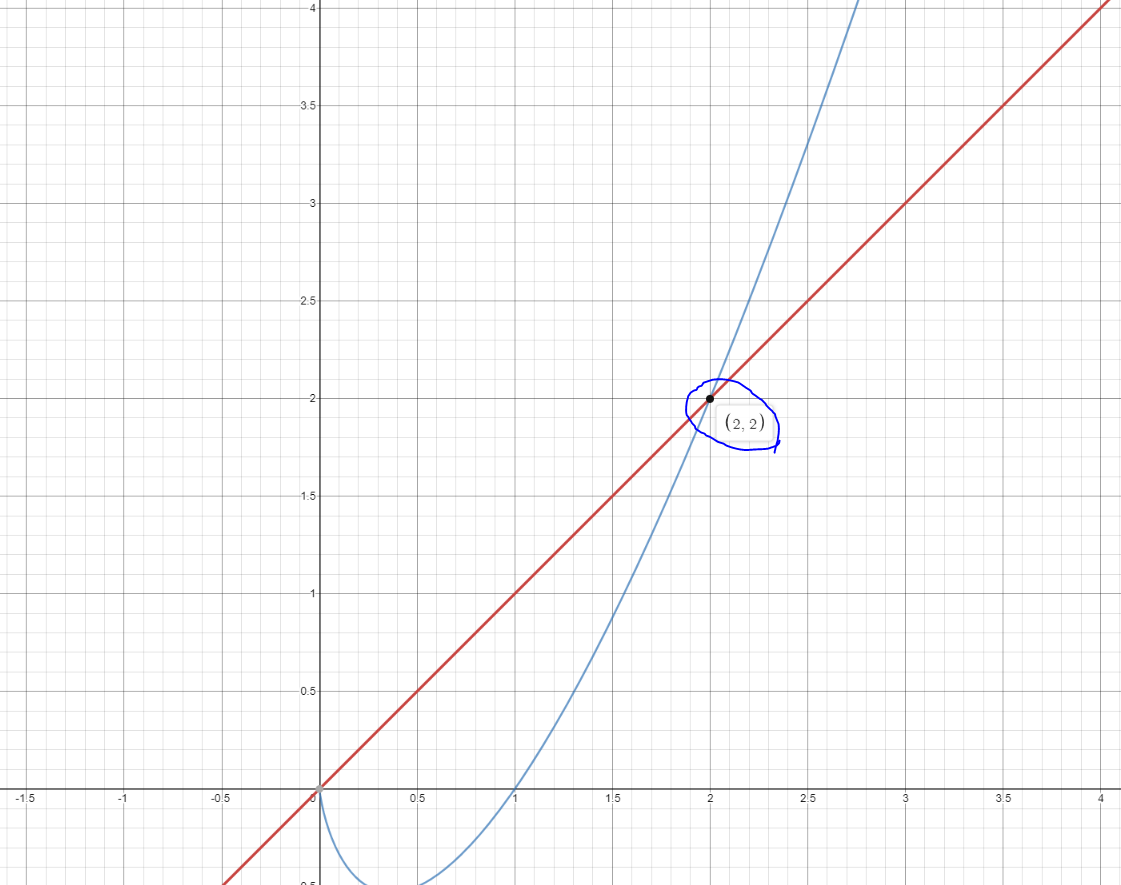
하지만 m이 늘어날 경우 m이 4라고 가정해보면

 

격차가 점점 줄어들다가 항목갯수가 16개 일 때 역전이 되는 것을 알 수 있습니다.

 

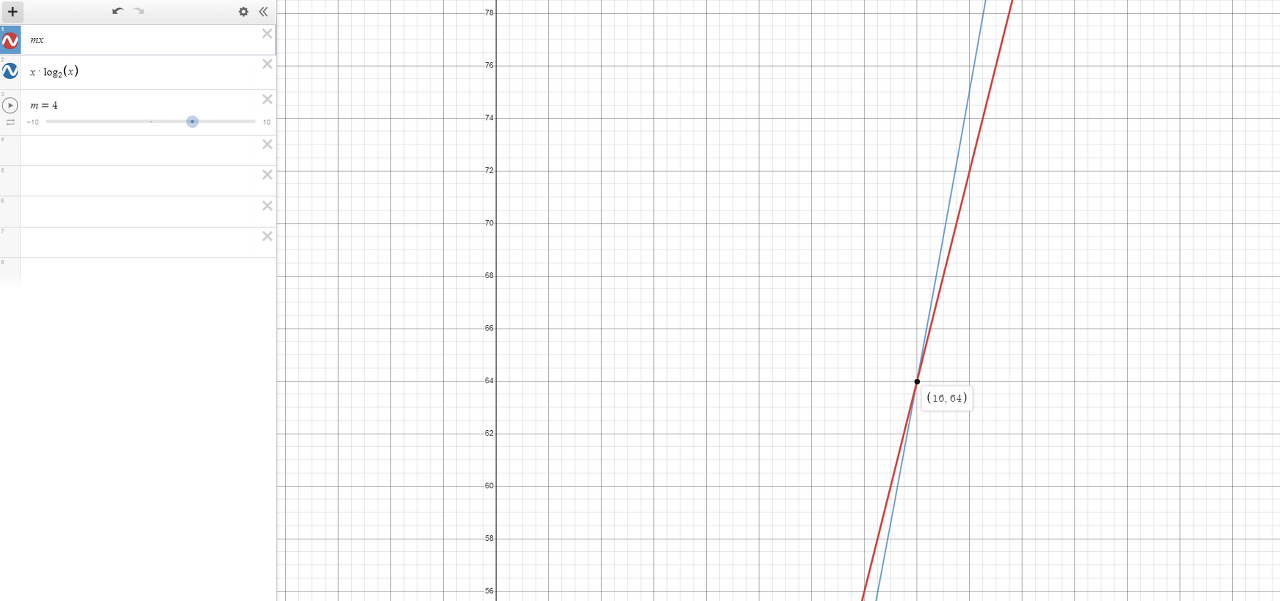
그러므로 일반적인 경우에 x * log2(x)이 더 느리지만 m이 커질 경우엔 x * log2(x)이 더 빨리 끝난다는 것을 알 수 있습니다.

이거보다 더 빠르게 끝나는 방법은 Heap을 사용하는 방법입니다. 그래서 최대 값, 최소 값, 몇 번째 큰 값이라는 문제가 있을 때 Heap을 사용해야 한다고 떠올려야 합니다.

푸는 방법은 큰 값을 찾을 때는 Min Heap을 사용하고, 작은 값을 찾을 때는 Max Heap을 사용합니다.

Input : [-1, 3, -1, 5, 4], 2

의 예시가 있을 때 Min Heap에 값을 넣으면 가장 작은 값이 위로 올라가게 됩니다.
그리고 3이 들어올 때 3이 더 작기 때문에 -1 Node의 자식 Node로 들어가게 됩니다.
그래서 이 Min Heap의 갯수를 2개만 유지 하는 것이죠.

 

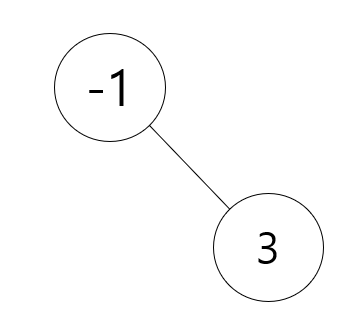
그랬을 때 -1을 또 넣게 되면 -1이 같으니까 밑에 집어 넣어 줍니다.

그렇게 되면 Tree가 3개가 되는데 2개가 될 때까지 빼버리게 됩니다.

 

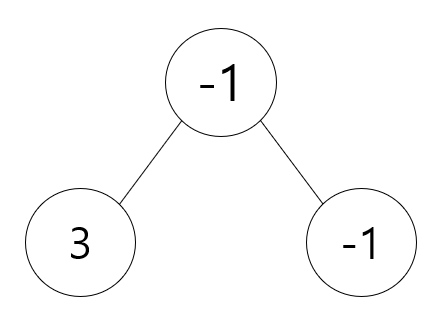
그러면 맨 위에 있는 -1을 빼버리고 자식 Node인 -1이 올라가니까 아래와 같아집니다.

 

그 다음 5를 집어 넣을 때 3과 5가 Swap되서 자리를 바꾸어 줍니다.

그 다음 4가 들어오게 되고 4는 3보다 크기 때문에 오른쪽 자식 Node로 들어오게 될 것이고,

3개가 되었기 때문에 3이 빠지고 4가 들어가 아래와 같이 됩니다.

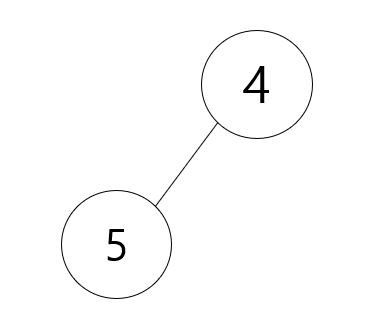
그랬을 때 맨 위에 있는 Root Node가 답이 됩니다. 이렇게 풀었을 때 어떤 이득이 있는지 살펴보죠.

각 배열의 요소를 돌면서 Heap에 Push를 하게 되고, 그 다음 Heap안에 자식의 갯수를 Count를 했을 때 찾고 싶은 값이 N일 때
Count는 N보다 큰 경우엔 Pop하게 됩니다. 그러니까 Count == N이 될 때 까지 Pop하게 됩니다.

그 다음 Push하고, Count가 N보다 크면 Pop하고, 다음노드로 넘어가는 형태를 반복하게 되죠.

저번 시간에 Heap에서 Push는 log2^N이라고 말했었습니다. Pop도 마찬가지로 log2^N입니다.

이렇게 보았을 때 배열의 갯수가 N개이고, Heap갯수 M인 Heap에 Push와 Pop을 한다 했을 때 Push, Pop을 한번씩 하게 되기 때문에 log2^M이 되고, 2번 반복해야 하니까 2 * log2^M이 되고, 이것을 N번 반복해야 하니까 2 * N log2^M이 됩니다.

 

그랬을 때 그래프로 그려보면 3번째 방법이 제일 빠르다는 것을 알 수 있습니다.

왜냐하면 항목이 늘어날 수록 M과 N의 격차는 벌어지기 때문 입니다.

 

정리해보면 배열이 있을 때 그 배열 안에 M번째 값을 찾습니다. 첫번째 값은 N개의 배열을 만든 다음에 각 항목을 다 비교하여 정렬해가며 하는 방법이 있고, 두 번째로 먼저 정렬을 한 다음에 M번째에 있는 값을 꺼내오는 방법이 있고, 세 번째 방법으로 Heap을 만들어서 M개의 Tree만 가질 수 있는 Heap을 만든 다음에 그 안에 항목을 넣고 빼고를 반복하는 방법이 있습니다.

 

그래서 알고리즘은 한가지 방법으로만 풀 수 있는 경우는 없고 그 중에 가장 최적인 것을 사용합니다.

 

이제 코드로 넘어와 구현을 해보죠.

 

heap.go로 와서 코드를 수정하는데 지난번에 만들었던 것은 MaxHeap입니다. 이것을 MinHeap으로 바꿔주는 방법은 부등호만 변경 시켜주면 됩니다.

기존에 있던 Push 부분과 Pop부분을 아래와 같이 부등호만 변경시켜주면 되지만 저 2개의 함수를 따로 만들었습니다.

func (h *Heap) MinHeap(v int) {
    h.list = append(h.list, v)

    idx := len(h.list) - 1
    for idx >= 0 {
        parantIdx := (idx - 1) / 2
        if parantIdx < 0 {
            break
        }
        if h.list[idx] < h.list[parantIdx] {
            h.list[idx], h.list[parantIdx] = h.list[parantIdx], h.list[idx]
            idx = parantIdx
        } else {
            break
        }
    }
}

func (h *Heap) MinHeapPop() int {
    if len(h.list) == 0 {
        return 0
    }

    top := h.list[0]
    last := h.list[len(h.list)-1]
    h.list = h.list[:len(h.list)-1]

    h.list[0] = last
    idx := 0

    for idx < len(h.list) {
        swapIdx := -1
        leftIdx := idx*2 + 1
        if leftIdx >= len(h.list) {
            break
        }
        if h.list[leftIdx] < h.list[idx] {
            swapIdx = leftIdx
        }

        rightIdx := idx*2 + 2
        if rightIdx < len(h.list) {
            if h.list[rightIdx] < h.list[idx] {
                if swapIdx < 0 || h.list[swapIdx] > h.list[rightIdx] {
                    swapIdx = rightIdx
                }
            }
        }

        if swapIdx < 0 {
            break
        }
        h.list[idx], h.list[swapIdx] = h.list[swapIdx], h.list[idx]
        idx = swapIdx
    }
    return top
}

이렇게 추가해준 뒤 main.go로 넘어와 코드를 수정해 줍니다.

package main

import (
    "fmt"

    "./dataStruct"
)

func main() {
    h := &dataStruct.Heap{}

    // [-1, 3, -1, 5, 4], 2번째 큰 값
    nums := []int{-1, 3, -1, 5, 4} // 1

  for i := 0; i < len(nums); i++ { // 2
    h.Push(nums[i])
  }
}

1 : nums라는 슬라이스를 생성한 뒤 그 안에 우리가 풀어야 할 수를 써 줍니다.
2 : for문을 사용하여 값들을 Heap에 Push해줍니다.

이제 heap의 count를 가져와야하는데 그 부분이 없기 때문에 count를 반환하는 함수를 써보죠!

heap.go

func (h *Heap) Count() int {
    return len(h.list)
}

이제 main부분을 이어서 작성해보죠!

func main() {
    h := &dataStruct.Heap{}

    // [-1, 3, -1, 5, 4], 2번째 큰 값
    nums := []int{-1, 3, -1, 5, 4}

  for i := 0; i < len(nums); i++ {
    h.MinHeap(nums[i])
    if h.Count() > 2 { // 1
      h.MinHeapPop()
    }
  }
  fmt.Println(h.MinHeapPop())
}

1 : count가 2개 이상이면 하나를 빼줍니다.

그리고 맨 위에 있는 값을 Pop을 해서 출력하면 2번째로 큰 값이 나오게 됩니다.

이제 실행시켜보죠!

이제 다른 문제도 풀어봅시다!

func main() {
    h := &dataStruct.Heap{}

    // [2, 4, -2, -3, 8], 1번째 큰 값
    nums := []int{2, 4, -2, -3, 8}

    for i := 0; i < len(nums); i++ {
        h.MinHeap(nums[i])
        if h.Count() > 1 {
            h.MinHeapPop()
        }
    }
    fmt.Println(h.MinHeapPop())
}

여기서 이렇게 실행하면 아래와 같은 오류가 뜹니다.

출력할 때 MinHeapPop을 하는데 이 갯수가 하나인데 MinHeapPop을 해서 list가 비어버리기 때문에 MinHeapPop()에서 자식Node를 맨 위로 올리는 과정이 있는데 그 자식Node가 없기 때문에 에러가 나게 되는 것입니다. MinHeapPop()코드를 수정해보죠!

heap.go

func (h *Heap) MinHeapPop() int {
    if len(h.list) == 0 {
        return 0
    }

    top := h.list[0]
    last := h.list[len(h.list)-1]
    h.list = h.list[:len(h.list)-1]

    if len(h.list) == 0 { // 수정된 부분.
        return top
    }

    h.list[0] = last
    idx := 0

    for idx < len(h.list) {
        swapIdx := -1
        leftIdx := idx*2 + 1
        if leftIdx >= len(h.list) { 
            break
        }
        if h.list[leftIdx] < h.list[idx] {
            swapIdx = leftIdx
        }

        rightIdx := idx*2 + 2
        if rightIdx < len(h.list) {
            if h.list[rightIdx] < h.list[idx] {
                if swapIdx < 0 || h.list[swapIdx] > h.list[rightIdx] {
                    swapIdx = rightIdx
                }
            }
        }

        if swapIdx < 0 {
            break
        }
        h.list[idx], h.list[swapIdx] = h.list[swapIdx], h.list[idx]
        idx = swapIdx
    }
    return top
}

이제 실행을 시키면

이제 그 아래에 코드를 더 추가하여 3번째 문제도 풀어보죠!

func main() {
    h := &dataStruct.Heap{}

    // [2, 4, -2, -3, 8], 1번째 큰 값
    nums := []int{2, 4, -2, -3, 8}

    for i := 0; i < len(nums); i++ {
        h.MinHeap(nums[i])
        if h.Count() > 1 {
            h.MinHeapPop()
        }
    }
    fmt.Println(h.MinHeapPop())

    // Input : [-5, 3, 1], 3번째 큰 값.
    nums = []int{-5, 3, 1}
    for i := 0; i < len(nums); i++ {
        h.MinHeap(nums[i])
        if h.Count() > 3 {
            h.MinHeapPop()
        }
    }
    fmt.Println(h.MinHeapPop())
}

정상적으로 나오는 것을 알 수 있다. 이 처럼 Heap을 사용해서 문제를 풀 수 있습니다.

 

풀소스

---

heap.go

package dataStruct

import "fmt"

type Heap struct {
 list []int
}

func (h *Heap) Push(v int) {
 h.list = append(h.list, v)

 idx := len(h.list) - 1
 for idx >= 0 {
  parentIdx := (idx - 1) / 2
  if parentIdx < 0 {
   break
  }
  if h.list[idx] < h.list[parentIdx] {
   h.list[idx], h.list[parentIdx] = h.list[parentIdx], h.list[idx]
   idx = parentIdx
  } else {
   break
  }
 }
}

func (h *Heap) Print() {
 fmt.Println(h.list)
}

func (h *Heap) Count() int {
 return len(h.list)
}

func (h *Heap) Pop() int {
 if len(h.list) == 0 {
  return 0
 }

 top := h.list[0]
 last := h.list[len(h.list)-1]
 h.list = h.list[:len(h.list)-1]

 if len(h.list) == 0 {
  return top
 }

 h.list[0] = last
 idx := 0
 for idx < len(h.list) {
  swapIdx := -1
  leftIdx := idx*2 + 1
  if leftIdx >= len(h.list) {
   break
  }
  if h.list[leftIdx] < h.list[idx] {
   swapIdx = leftIdx
  }

  rightIdx := idx*2 + 2
  if rightIdx < len(h.list) {
   if h.list[rightIdx] < h.list[idx] {
    if swapIdx < 0 || h.list[swapIdx] > h.list[rightIdx] {
     swapIdx = rightIdx
    }
   }
  }

  if swapIdx < 0 {
   break
  }
  h.list[idx], h.list[swapIdx] = h.list[swapIdx], h.list[idx]
  idx = swapIdx
 }
 return top
}

 

main.go

package main

import (
 "dataStruct"
 "fmt"
)

func main() {
 h := &dataStruct.Heap{}

 // [-1, 3, -1, 5, 4], 2번째 큰값
 nums := []int{-1, 3, -1, 5, 4}

 for i := 0; i < len(nums); i++ {
  h.Push(nums[i])
  if h.Count() > 2 {
   h.Pop()
  }
 }
 fmt.Println(h.Pop())

 //Input: [2, 4, -2, -3, 8], 1
 //Output: 8
 h = &dataStruct.Heap{}

 nums = []int{2, 4, -2, -3, 8}

 for i := 0; i < len(nums); i++ {
  h.Push(nums[i])
  if h.Count() > 1 {
   h.Pop()
  }
 }
 fmt.Println(h.Pop())

 //Input: [-5, -3, 1], 3
 //Output: -5
 h = &dataStruct.Heap{}

 nums = []int{-5, -3, 1}

 for i := 0; i < len(nums); i++ {
  h.Push(nums[i])
  if h.Count() > 3 {
   h.Pop()
  }
 }
 fmt.Println(h.Pop())
}