[바미] 알고리즘 시간 복잡도 용어 정리
들어가기전에..
안녕하세요. 요즘 매일 매일 제가 백준 알고리즘을 푼 것을 '하루 알고리즘'이라는 컨텐츠로 포스팅 하고 있습니다.
'하루 알고리즘(JS)' 카테고리의 글 목록
안녕하세요. 4년차 백엔드 개발자로 활동하고 있습니다. 코딩과 무관한 것들과 유관한 부분들 모두 공유 합니다. 오타나, 틀린 부분이 있다면 언제든지 지적 환영 입니다.
codesk.tistory.com
여기서 시간 복잡도 관련 용어들을 정리해보면 좋을 것 같아 이번 글을 포스팅하게 되었습니다.
빅오 표기법?
빅오 표기법은 알고리즘의 효율성을 표현하기 위해 사용되는 표기법입니다.
알고리즘의 단계 수는 입력 크기에 따라 달라지기 때문에 '배열에 N개의 원소가 있을 때 N단계가 필요하다'와 같이 표현하는 것이 더 효과적이죠.
컴퓨터 과학자들은 자료 구조와 알고리즘의 효율성을 설명하기 위해 수학적 개념을 차용하여 빅오 표기법을 사용합니다.
이를 통해 알고리즘의 시간 복잡도를 일관되고 간결한 언어로 표현하고 분석할 수 있습니다.
빅오 표기법을 통해 알고리즘의 효율성을 쉽게 소통할 수 있으며, 이는 알고리즘을 비교하고 평가하는 데 중요한 도구가 됩니다.
빅오 표기법을 쓰는 이유
위에 설명했던 '알고리즘의 효율성을 쉽게 소통할 수 있으며, 이는 알고리즘을 비교하고 평가하는 데 중요한 도구'를 뒷받침 하여 설명해보겠습니다.
알고리즘의 효율성은 수행에 필요한 단계 수로 결정되지만 이 단계 수는 입력 데이터의 크기에 따라 변하기 때문 알고리즘을 "22단계" 또는 "400단계"라고 단순히 표시할 수 없습니다.
예를 들어, 선형 검색의 경우 배열의 원소 개수만큼 단계가 필요합니다. 원소가 4개일 때는 4단계, 100개일 때는 100단계가 필요하므로, 이를 'N개의 원소가 있을 때 N단계가 필요하다'고 표현하는 것이 더 효과적인 것이죠.
빅오 표기법의 필요성
빅오 표기법은 크게 3가지를 의미합니다.
- 데이터 원소 N개에 대한 알고리즘의 단계 수
- 데이터가 늘어날 때 단계 수가 어떻게 증가하는지
- 최악의 시나리오
이 부분을 자세히 알아보도록 하겠습니다.
1. 데이터 원소 N개에 대한 알고리즘 단계 수
빅오 표기법의 핵심 질문은 '데이터 원소가 N개일 때 알고리즘에 몇 단계가 필요한가?'입니다.
예를 들어 O(N)은 N단계가 필요함을 의미하는데 입력 크기와 단계 수 간의 관계를 명확히 설명합니다.
2. 데이터가 늘어날 때 단계 수가 어떻게 증가하는지
데이터가 늘어날 때 단계 수가 어떻게 증가하는지도 설명해줍니다.
아래는 예시입니다.
O(1) 알고리즘(상수 시간을 갖는 알고리즘)
- 데이터 크기에 상관없이 항상 일정한 단계 수 증가 (예: 배열의 첫 번째 원소 접근).
O(N) 알고리즘(선형 시간을 갖는 알고리즘)
- 데이터 크기에 비례하여 단계 수 증가 (예: 선형 검색).
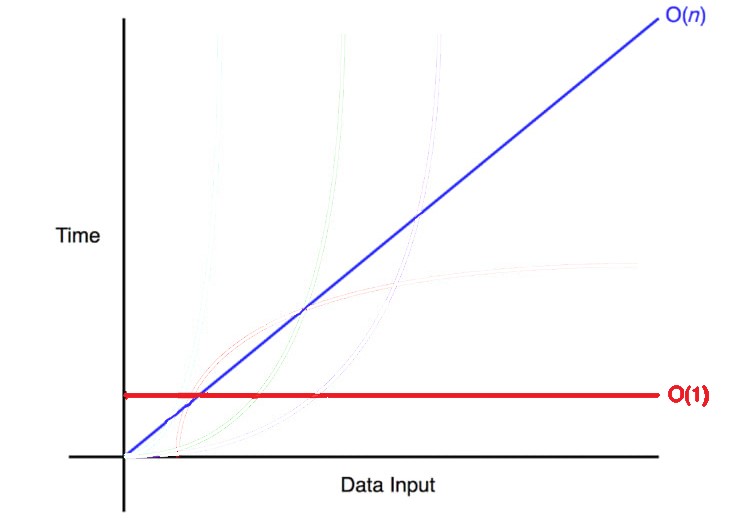
데이터가 하나씩 추가될 때마다 알고리즘이 한 단계씩 더 걸리기 때문에 O(N)은 완벽한 대각선을 그리고 있습니다.
데이터가 많아질수록 알고리즘에 필요한 단계 수도 늘어난다는 것을 의미하죠.
반면에 O(1)은 완벽한 수평선을 그리게 되는데 데이터의 증가나 감소에 영향 받지 않고 단계 수가 일정하다는 것을 의미합니다.
그럼 O(1)알고리즘이 항상 O(N)보다 빠를까요?
데이터 크기에 상관없이 항상 100단계가 걸리는 상수 시간 알고리즘이 있다면 이 알고리즘이 O(N) 알고리즘보다 성능이 우수할까요?
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>O(1) vs O(N) Algorithm Comparison</title>
<script src="https://d3js.org/d3.v6.min.js"></script>
<style>
.line {
fill: none;
stroke-width: 2px;
}
.axis-label {
font-size: 12px;
}
</style>
</head>
<body>
<h2>O(1) 알고리즘과 O(N) 알고리즘의 단계 수 비교</h2>
<svg id="chart" width="800" height="500"></svg>
<script>
const width = 800;
const height = 500;
const margin = { top: 20, right: 20, bottom: 30, left: 50 };
const svg = d3.select("#chart")
.attr("width", width)
.attr("height", height);
const x = d3.scaleLinear()
.domain([0, 200])
.range([margin.left, width - margin.right]);
const y = d3.scaleLinear()
.domain([0, 200])
.range([height - margin.bottom, margin.top]);
const xAxis = g => g
.attr("transform", `translate(0,${height - margin.bottom})`)
.call(d3.axisBottom(x).ticks(width / 80))
.call(g => g.append("text")
.attr("x", width - 4)
.attr("y", -4)
.attr("fill", "currentColor")
.attr("font-weight", "bold")
.attr("text-anchor", "end")
.text("데이터 세트의 원소 수 (N)"));
const yAxis = g => g
.attr("transform", `translate(${margin.left},0)`)
.call(d3.axisLeft(y))
.call(g => g.append("text")
.attr("x", 4)
.attr("y", 10)
.attr("fill", "currentColor")
.attr("font-weight", "bold")
.attr("text-anchor", "start")
.text("단계 수"));
svg.append("g").call(xAxis);
svg.append("g").call(yAxis);
const lineO1 = d3.line()
.x((d, i) => x(i + 1))
.y(d => y(d));
const lineON = d3.line()
.x((d, i) => x(i + 1))
.y((d, i) => y(i + 1));
const dataO1 = Array(200).fill(100);
const dataON = Array.from({ length: 200 }, (_, i) => i + 1);
svg.append("path")
.datum(dataO1)
.attr("class", "line")
.attr("d", lineO1)
.attr("stroke", "blue");
svg.append("path")
.datum(dataON)
.attr("class", "line")
.attr("d", lineON)
.attr("stroke", "red");
svg.append("line")
.attr("x1", x(100))
.attr("y1", y(0))
.attr("x2", x(100))
.attr("y2", y(200))
.attr("stroke", "green")
.attr("stroke-dasharray", "4");
svg.append("line")
.attr("x1", x(0))
.attr("y1", y(100))
.attr("x2", x(200))
.attr("y2", y(100))
.attr("stroke", "grey")
.attr("stroke-dasharray", "4");
svg.append("text")
.attr("x", x(100))
.attr("y", y(200) + 15)
.attr("text-anchor", "middle")
.attr("fill", "green")
.text("교차 지점 (N=100)");
svg.append("text")
.attr("x", x(200) - 10)
.attr("y", y(100) - 5)
.attr("text-anchor", "end")
.attr("fill", "grey")
.text("100단계");
</script>
</body>
</html>

이 그래프를 보면 알 수 있듯이 원소가 100개 이하인 데이터 세트에서는 O(1) 알고리즘이 항상 100단계가 걸리는 반면
O(N) 알고리즘은 원소의 수(N)에 비례하여 단계 수가 결정됩니다. 즉, 원소가 100개 이하인 경우, O(N) 알고리즘의 단계 수는 최대 100단계입니다.
하지만 원소의 수가 정확히 100개일 때는 두 알고리즘의 단계 수가 동일하게 100단계가 됩니다. 원소가 100개를 초과하면 O(N) 알고리즘의 단계 수는 100단계를 초과하게 되므로, O(1) 알고리즘보다 덜 효율적이 되는데 이 지점이 바로 두 알고리즘의 성능이 교차하는 지점입니다.
결국, 원소의 수가 100보다 큰 모든 배열에서는 O(N) 알고리즘이 O(1) 알고리즘보다 더 많은 단계가 걸립니다. 이로 인해 O(N) 알고리즘이 O(1) 알고리즘보다 덜 효율적이라고 할 수 있습니다.
3. 최악의 시나리오
특정 알고리즘이 가장 많은 자원을 소비하는 경우를 의미하며, 이를 통해 알고리즘의 효율성을 평가할 수 있습니다.
예를 들어, 선형 검색(linear search)은 배열에서 특정 값을 찾는 알고리즘입니다. 이 알고리즘의 시간 복잡도는 다음과 같이 두 가지 시나리오로 나뉩니다.
- 최선의 시나리오 (Best Case): 검색값이 배열의 첫 번째 위치에 있는 경우.
이 경우 알고리즘은 단 한 번의 비교만으로 값을 찾을 수 있으므로, 시간 복잡도는 O(1)입니다. - 최악의 시나리오 (Worst Case): 검색값이 배열의 마지막 위치에 있거나 배열에 존재하지 않는 경우.
이 경우 배열의 모든 요소를 비교해야 하므로, 시간 복잡도는 O(N)입니다.
알고리즘 분석에서 '비관적인' 접근은 알고리즘의 신뢰성과 효율성을 평가하는 데 필수적인 도구입니다.
이를 통해 더 나은 시스템을 설계하고, 예기치 않은 상황에서도 시스템의 안정성을 유지할 수 있습니다.
빅 오 표기법(Big O Notation)
빅 오 표기법은 알고리즘의 시간 복잡도를 나타내는 수학적 표기법입니다.
O(N) - 선형 시간 (Linear Time)
O(N) 표기법은 데이터 원소의 수 N에 정확히 비례해 단계 수가 증가하는 알고리즘을 나타냅니다.
O(1) - 상수 시간 (Constant Time)
O(1) 표기법은 데이터 원소의 수와 상관없이 항상 일정한 단계 수만 걸리는 알고리즘을 나타냅니다.
배열에서 특정 원소를 읽는 작업이 대표적입니다.
로그(log)
로그는 지수와 역의 관계를 나타내는 개념입니다. 예를 들어, 2를 몇 번 곱해야 N이 되는지를 나타내는 것이 log₂N입니다.
로그의 예시
- 2를 몇 번 곱해야 8이 나오는가?
- log₂8 = 3 (2³ = 8)
- 2를 몇 번 곱해야 64가 나오는가?
- log₂64 = 6 (2⁶ = 64)
O(logN) - 로그 시간 (Logarithmic Time)
O(logN) 표기법은 데이터 원소가 N개 있을 때 알고리즘이 log₂N 단계가 걸리는 것을 나타냅니다. 이진 검색 알고리즘이 그 예 입니다.
이진 검색의 단계 수 예시
- 배열의 크기가 3일 때: 2단계
- 배열의 크기가 7일 때: 3단계
- 배열의 크기가 15일 때: 4단계
- 배열의 크기가 100일 때: 7단계
- 배열의 크기가 10,000일 때: 13단계
- 배열의 크기가 1,000,000일 때: 20단계
이진 검색은 데이터가 커질수록 단계 수가 증가하지만, 원소 수보다는 훨씬 적은 단계 수로 검색이 가능하기 때문에 O(logN)으로 표현합니다.
| O(N) | O(1) | O(log N) |
| 선형 시간 | 상수 시간 | 로그 시간 |
| 데이터 양에 비례하여 단계 수 증가 | 데이터 양에 상관없이 일정한 단계 수 | 데이터가 두 배로 증가할 때마다 한 단계씩 증가 |
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>Big O Notation Graph</title>
<style>
canvas {
border: 1px solid black;
}
</style>
</head>
<body>
<canvas id="bigOCanvas" width="600" height="400"></canvas>
<script>
const canvas = document.getElementById('bigOCanvas');
const ctx = canvas.getContext('2d');
// Set up canvas
ctx.clearRect(0, 0, canvas.width, canvas.height);
// Define colors
const colors = {
O1: 'black',
OlogN: 'red',
ON: 'blue'
};
// Draw axes
function drawAxes() {
ctx.beginPath();
ctx.moveTo(50, 350);
ctx.lineTo(550, 350); // X-axis
ctx.moveTo(50, 350);
ctx.lineTo(50, 50); // Y-axis
ctx.strokeStyle = 'black';
ctx.stroke();
}
// Draw labels
function drawLabels() {
ctx.font = '14px Arial';
ctx.fillText('Data Input', 280, 380);
ctx.fillText('Time', 10, 200);
ctx.fillText('O(1)', 550, 115);
ctx.fillText('O(log N)', 80, 150);
ctx.fillText('O(N)', 550, 65);
}
// Draw O(1) line
function drawO1() {
ctx.beginPath();
ctx.moveTo(50, 100);
ctx.lineTo(550, 100);
ctx.strokeStyle = colors.O1;
ctx.stroke();
}
// Draw O(log N) curve
function drawOlogN() {
ctx.beginPath();
for (let x = 50; x <= 550; x++) {
const y = 350 - 50 * Math.log2(x - 49);
if (x === 50) {
ctx.moveTo(x, y);
} else {
ctx.lineTo(x, y);
}
}
ctx.strokeStyle = colors.OlogN;
ctx.stroke();
}
// Draw O(N) line
function drawON() {
ctx.beginPath();
ctx.moveTo(50, 350);
ctx.lineTo(550, 50);
ctx.strokeStyle = colors.ON;
ctx.stroke();
}
// Draw graph
drawAxes();
drawLabels();
drawO1();
drawOlogN();
drawON();
</script>
</body>
</html>

그래프로 보았을 때 O(1) > O(logN) > O(N) 순으로 가장 효율적인 것을 알 수 있습니다.